
- •Числовые ряды Числовой ряд. Общий член ряда
- •Сходящиеся и расходящиеся ряды
- •Основные свойства сходящихся рядов
- •Признаки сходимости числовых рядов
- •Необходимый признак сходимости ряда
- •Если , то ряд расходится.
- •Знакоположительные числовые ряды
- •Достаточные признаки сходимости знакоположительных рядов
- •Знакочередующиеся и знакопеременные ряды Знакочередующиеся ряды
- •Знакопеременные ряды
- •Функциональные ряды Функциональный ряд и его область сходимости
- •Степенные ряды
- •Геометрическая интерпретация теоремы Абеля
- •Разложение элементарных функций в степенные ряды
- •Приближенные вычисления с помощью степенных рядов
- •Приближенное вычисление корней
- •Приближенное вычисление определенных интегралов
- •Приближенное решение дифференциальных уравнений
- •Теоретические вопросы
- •Расчетные задания
Функциональные ряды Функциональный ряд и его область сходимости
Пусть
![]() ,
,
![]() ,...,
,...,![]() ,...
–
последовательность функций, определенных
на некотором множестве
,...
–
последовательность функций, определенных
на некотором множестве
![]() .
.
Определение Ряд вида
![]() ,
,
членами которого являются функции, называется функциональным.
Придавая
![]() различные числовые значения из множества
различные числовые значения из множества
![]() ,
будем получать различные числовые ряды.
В частности, при
,
будем получать различные числовые ряды.
В частности, при
![]() функциональный ряд становится числовым
рядом
функциональный ряд становится числовым
рядом
![]() .
Этот числовой ряд может быть сходящимся
или расходящимся. Если он сходится, то
.
Этот числовой ряд может быть сходящимся
или расходящимся. Если он сходится, то
![]() называется точкой
сходимости функционального ряда.
называется точкой
сходимости функционального ряда.
Множество
всех точек сходимости функционального
ряда называют его
областью
сходимости
и обозначают ее через
![]() .
Очевидно,
.
Очевидно,
![]() .
В частных случаях множество
.
В частных случаях множество
![]() может совпадать или не совпадать с
множеством
или же может быть и пустым множеством.
В последнем случае функциональный ряд
расходится в каждой точке множества
.
может совпадать или не совпадать с
множеством
или же может быть и пустым множеством.
В последнем случае функциональный ряд
расходится в каждой точке множества
.
Вид области для произвольного функционального ряда может быть различным: вся числовая ось, интервал, объединение интервалов и полуинтервалов и т.д. В простейших случаях при исследовании функциональных рядов на сходимость можно применить рассмотренные выше признаки сходимости числовых рядов, если под x понимать фиксированное число.
Определения.
Сумма
первых
членов функционального ряда
![]() называется
называется
![]() ой
частичной суммой,
а функция
ой
частичной суммой,
а функция
![]() ,
определенная в области
,–
суммой
функционального ряда.
Функция
,
определенная в области
,–
суммой
функционального ряда.
Функция
![]() ,
определенная в области
,
называется остатком
ряда.
Функциональный ряд называется абсолютно
сходящимся
на множестве
,
если в каждой точке
сходится ряд
,
определенная в области
,
называется остатком
ряда.
Функциональный ряд называется абсолютно
сходящимся
на множестве
,
если в каждой точке
сходится ряд
![]() .
.
Степенные ряды
Частным случаем функциональных рядов являются степенные ряды.
Определение Степенным рядом называется функциональный ряд
![]() ,
,
члены
которого являются произведениями
постоянных
![]() ,
,
![]() ,
...,
,
...,
![]() ,...
на степенные функции от разности
,...
на степенные функции от разности
![]() с целыми неотрицательными показателями
степеней, точка x0
называется
центром
степенного ряда.
с целыми неотрицательными показателями
степеней, точка x0
называется
центром
степенного ряда.
Пример
19.
Ряд
![]() – степенной ряд с центром в точке
– степенной ряд с центром в точке
![]() .
.
Ряд
![]() – степенной ряд с центром в точке
– степенной ряд с центром в точке
![]() .
.
Ряд
![]() – функциональный ряд.
– функциональный ряд.
Исследование степенного ряда на сходимость, а именно нахождение области сходимости степенного ряда, является одним из главных вопросов. Решение этого вопроса связано с теоремой Абеля.
Теорема (Абеля)
Если степенной ряд сходится при
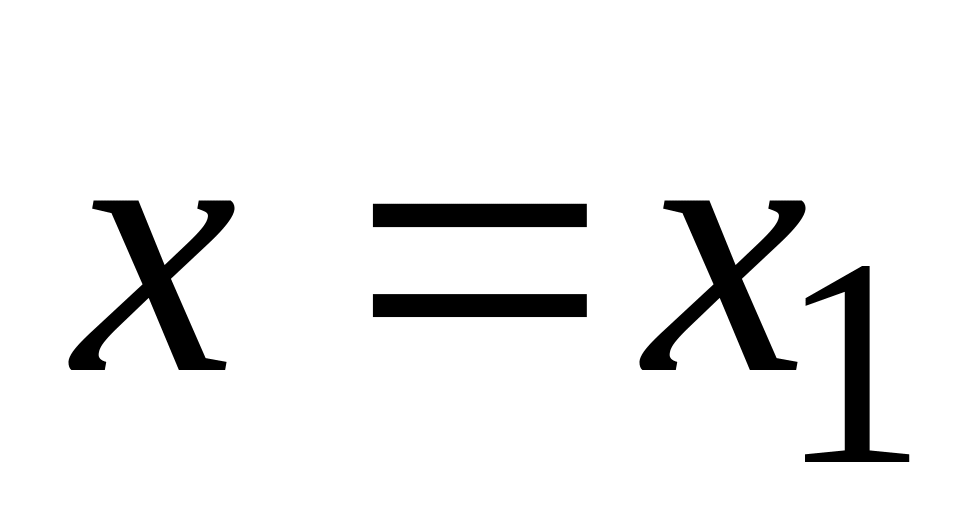
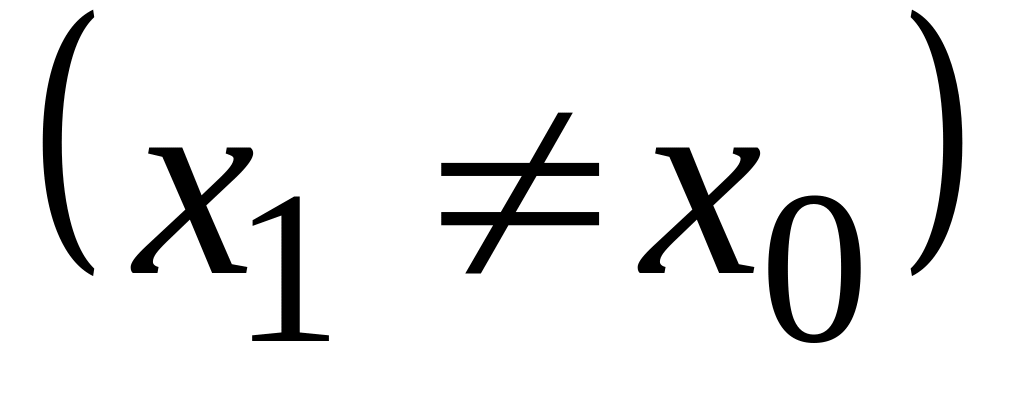 ,
то он сходится, и притом абсолютно, для
всех
,
то он сходится, и притом абсолютно, для
всех
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() .
.
Если степенной ряд расходится при
 ,
то он расходится для всех
,
удовлетворяющих неравенству
,
то он расходится для всех
,
удовлетворяющих неравенству
![]() .
.
Геометрическая интерпретация теоремы Абеля
Если
степенной ряд сходится в точке
![]() ,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда
,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда
![]() ,
чем
,
чем
![]() .
Если же ряд расходится при
.
Если же ряд расходится при
![]() ,
то он расходится и во всех более удаленных
от центра ряда точках.
,
то он расходится и во всех более удаленных
от центра ряда точках.
Опираясь
на теорему Абеля можно доказать, что
существует такое положительное число
![]() ,
что для всех
,
удовлетворяющих неравенству
,
что для всех
,
удовлетворяющих неравенству
![]() ,
ряд сходится абсолютно и расходится
при всех
,
для которых
,
ряд сходится абсолютно и расходится
при всех
,
для которых
![]() .
.
Число
![]() называется радиусом
сходимости
ряда
называется радиусом
сходимости
ряда
![]() ,
а интервал
,
а интервал
![]() – интервалом
сходимости.
– интервалом
сходимости.
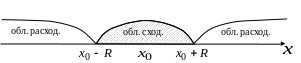
В
частном случае интервал сходимости
степенного ряда может совпадать со всей
числовой осью (в этом случае
![]() )
или может превращаться в точку (в этом
случае
)
или может превращаться в точку (в этом
случае
![]() ).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
Если
для степенного ряда существует
![]() ,
то радиус сходимости степенного ряда
можно вычислить по формуле
,
то радиус сходимости степенного ряда
можно вычислить по формуле
![]()
Рассмотрим способы определения области сходимости степенного ряда на примерах.
Пример
20.
Найти интервал сходимости степенного
ряда
![]() .
.
Первый способ решения
Рассмотрим
ряд, составленный из абсолютных величин
членов данного ряда:
![]() .
Применим признак Даламбера:
.
Применим признак Даламбера:
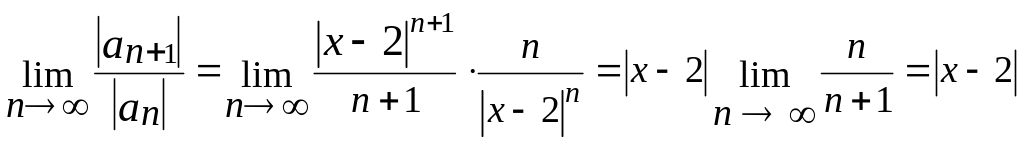 .
.
Если
![]() ,
то ряд сходится. Итак,
,
то ряд сходится. Итак,
![]() ,
,
![]() –
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках
–
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках
![]() и
и
![]() ,
исследуется отдельно.
,
исследуется отдельно.
При
из данного ряда получаем ряд
![]() ,
который условно сходится.
,
который условно сходится.
При получаем гармонический ряд , который расходится.
Таким образом, данный ряд сходится в области, для которой .
Второй способ решения
В
нашем случае
![]() и
и
![]() ,
поэтому
,
поэтому
![]() .
.
Так
как
![]() – центр степенного ряда, то
– центр степенного ряда, то
![]() – интервал сходимости данного ряда.
– интервал сходимости данного ряда.
Сходимость ряда на концах интервала сходимости исследована выше.
Итак, данный ряд сходится абсолютно при и условно при .
