2.4. Двигатель постоянного тока как

динамическое звено

Для того, чтобы оценить динамические характеристики электроприводов на базе двигателей постоянного тока с независимым возбуждением составим структурную схему данного двигателя.

Электромеханические процессы при постоянном потоке возбуждения описываются следующей системой уравнений:

(2.11)

Электромагнитная и механическая инерционности двигателя отражаются соответственно электромагнитной T_a и электромеханической T_М постоянными времени. Для двигателя постоянного тока

, (2.12)

, (2.13)

Решая уравнения (2.11) с учетом (2.12) и (2.13) получим

, (2.14)

где: .

Мы видим, что полученное уравнение совпадает с уравнением для двигателей с линейной механической характеристикой, вид которой определяется величиной ее жесткости .

Переходя к операторной форме записи, полагая , получим исходную для построения структурной схемы систему уравнений:

. (2.15)

Данная система уравнений отражается структурной схемой, состоящей из типовых динамических звеньев (рис. 2.3).

Рис. 2.3. Структурная схема двигателя постоянного тока

при постоянном потоке возбуждения

Механическая часть двигателя, характеризуется интегрирующим звеном с постоянной времени T_м, величина которой определяется суммой момента инерции якоря двигателя и моментом инерции всех движущихся частей рабочей машины, приведенными к валу двигателя. Электромеханическое преобразование энергии отражается пропорциональным звеном коэффициента передачи кФ, которое указывает, что момент двигателя пропорционален току якоря. Электрическая цепь якоря двигателя представлена инерционным звеном с постоянной времени T_a. Это звено характеризует как изменяется ток якоря при изменении разности напряжений (U_a – E_a). ЭДС якоря E_a=кФ отражается в виде отрицательной обратной связи. Такая связь является внутренней, т.к. она соответствует природе физических процессов в описываемом объекте, а не создана системой регулирования.

Передаточная функция двигателя по управляющему воздействию при регулировании скорости изменением напряжения якоря будет:

(2.16)

Здесь С = кФ – машинная постоянная при неизменном потоке возбуждения.

Характер переходных процессов определяется видом корней характеристического уравнения, левая часть которого – знаменатель передаточной функции (2.16).

Характеристическое уравнение, определяющее свободную составляющую переходного процесса, запишем в виде:

T_aТ_мp² + T_мp + 1 = 0.

Корни этого уравнения

.

Если 4T_a < Т­_M, двигатель может быть представлен двумя последовательно включенными инерционными звеньями с передаточной функцией:

, (2.17)

где T₁, T₂ определяют из системы уравнений

.

Если 4Т_a > T_м, двигатель эквивалентен колебательному звену с передаточной функцией (2.16).

Выражение переходной характеристики для тока I_a = f(t) может быть получено из уравнения движения (2.1). Получим

(2.18)

т.е. ток является суммой двух составляющих: статического тока и динамического тока, который по своему характеру является производной от скорости.

Передаточную функцию для тока при управляющем воздействии найдем из структурной схемы (рис. 2.3)

(2.19)

где: I_c – статический ток, соответствующий статическому моменту.

На рис. 2.4. показаны переходные характеристики скорости и тока при пуске двигателя до некоторой скорости при наличии на валу двигателя реактивного статического момента; Будем полагать, что в рассматриваемом случае Т_м > 4T_a. В течении времени t₀ ток якоря нарастает до значения . Нарастание происходит по экспоненциальному закону .

Когда ток станет равным статическому, начинается движение вала двигателя. Динамический ток возрастает, вследствие чего растет ускорение двигателя. Затем под действием увеличивающейся противоэдс якоря ток начинает спадать, и скорость двигателя асимптотически приближается к установившемуся значению.

Рис. 2.4. Графики переходных характеристик для тока и скорости

а) при T_м > T­_a; б) при T_м < 4Т_a

Если Tм < 4Т_a, то в кривых тока и скорости появится колебательная составляющая (см. рис. 2.4.б).

Рассмотрим теперь динамические процессы при приложении нагрузки к валу двигателя при постоянном напряжении, подводимом к якорной цепи двигателя. Структурная схема для этого случая представлена на рис. 2.5, а переходные характеристики – на рис. 2.6. Примем, что двигатель работал вхолостую со скоростью , ток якоря I_a = 0, т.к. приложенное напряжение уравновешивалось ЭДС якоря U_a = E_a.

Рис. 2.5. Структурная схема двигателя постоянного тока независимого

возбуждения при приложение возмущения по нагрузке.

Если к валу двигателя скачком приложить нагрузку – статический момент M_с=кФI_c то скорость двигателя начнет снижаться, ЭДС якоря будет уменьшаться и в цепи якоря начнет нарастать ток.

.

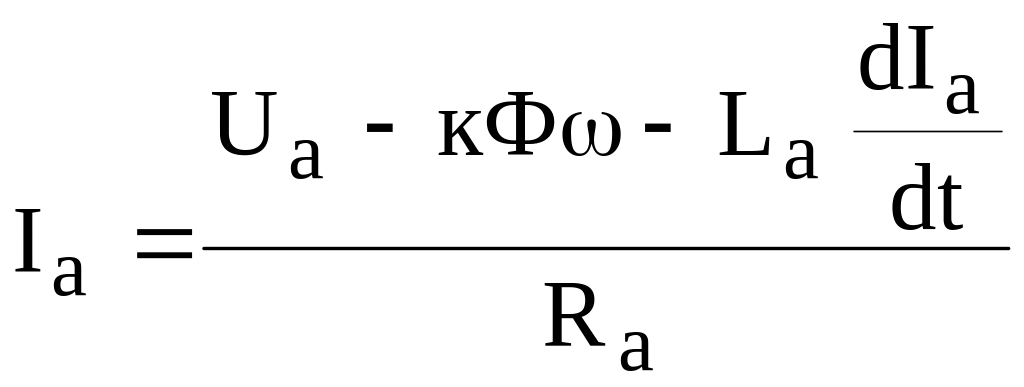Если индуктивность якорной цепи велика (постоянная времени ), то нарастание тока будет отставать от темпа снижения скорости и к моменту, когда скорость снизится до нового установившегося значения , ток якоря еще не достигнет величины I_с, при которой момент двигателя был бы равен моменту сопротивления М_с. Поэтому скорость будет продолжать падать до тех пор, пока ток якоря не станет равен статическому, затем скорость начнет возрастать и после ряда колебаний достигнет установившегося значения. Обратим внимание, что кривые  = f(t) и I_a=f(t) взаимосвязаны – точкам максимума и минимума скорости, когда , соответствует момент пересечений кривой тока, линии статического тока.

Рис. 2.6. Переходные характеристики тока и

скорости при приложении нагрузки

Если индуктивность якорной цепи невелика то процесс снижения скорости при приложении нагрузки будет иметь монотонный характер.

Передаточные функции двигателя постоянного тока при возмущении по нагрузке будут

, (2.20)

. (2.21)

При изменении потока возбуждения электромеханические переходные процессы в двигателе постоянного тока будут описываться системой нелинейных дифференциальных уравнений, т.к. в уравнениях (2.11) присутствуют произведения переменных.

Аналитическое решение системы в этом случае сопряжено с математическими трудностями. Для анализа процессов при одновременном управлении и напряжением якоря и током возбуждения удобно использовать математическое моделирование электромеханических процессов на компьютере на основе структурной схемы, представленной на рис. 2.7.

Рис. 2.7. Структурная схема двигателя постоянного тока по цепи якоря и

цепи возбуждения

Быстродействие управления по цепи якоря определяется, главным образом, электромагнитной постоянной времени якорной цепи, которая невелика и составляет обычно 0.02 – 0.1 с. Постоянная времени обмотки возбуждения гораздо больше и составляет 0.5 – 3 с, что определяет существенно меньшее быстродействие при регулировании скорости воздействием на поток возбуждения. Кроме того, скорость изменения магнитного потока снижается из-за наличия контура вихревых токов, что в схеме рис. 2.7 учтено постоянной времени T_вт, которая может составлять 0.15-0.30 с.

На схеме рис. 2.7 показаны в виде динамических звеньев источники регулируемого напряжения в цепях питания цепей якоря и обмотки возбуждения – тиристорные преобразователи ТПA и ТПВ.