2.2. Структурные схемы механической части электропривода

При деформации упругих звеньев происходит рассеяние (диссипация) механической энергии, обусловленное силами внутреннего трения, называемыми диссипативными силами, величина которых пропорциональна разности скоростей перемещения соседних дискретных масс. Диссипативные силы в упругих связях, как правило, существенно меньше потенциальных сил, в связи с чем при исследовании законов движения электроприводов механизмов в первом приближении, можно не учитывать. С учетом указанных допущений, а также того, моменты инерций постоянны и _д = ₁, можно записать уравнения движения в случае вращательной схемы приведения:

для одномассовой системы

Jd₁/dt = M_дв – M_c, (2.1)

для двухмассовой системы

, (2.2)

для трехмассовой системы

. (2.3)

Структурные схемы механической части электропривода соответствующие приведенным уравнениям (2.1) – (2.3) показаны на рис. 2.1

Рис. 2.1. Структурные схемы одномассовой (а), двухмассовой (б)

и трехмассовой (в) систем

Аналогично могут быть составлены уравнения движения и структурные схемы для поступательно движущейся системы.

Передаточные функции для одномассовой, двухмассовой и трехмассовой систем имеют вид соответственно:

; (2.4)

; (2.5)

, (2.6)

где J_2 = J₁ + J₂, J_3 = J₁ + J₂ + J₃, T₁ = J₁J₂/c₁₂J_2, T₂ = J₁J₂J₃/c₁₂c₂₃J_3,

- коэффициенты передаточных функций.

Многомассовые системы представляют собой колебательные системы с резонансными частотами:

для двухмассовой

, (2.7)

для трехмассовой

, (2.8)

где: ; ; - собственные частоты колебаний соответствующих звеньев; ₁ = J₁ / J₂, ₂ = J₃ / J₂ – отношения моментов инерции.

На этих частотах (2.7), (2.8) может возникнуть явление механического резонанса, связанное с резким возрастанием амплитуды движения масс системы. Анализ такого движения достаточно сложен и приводится в фундаментальных трудах по теории электропривода.

2.3. Обобщенная структурная схема механической

части электропривода

За основу обобщенной структурной схемы принята двухмассовая упругая механическая система, которая принципиально полно отражает физические особенности реальных систем и в то же время является предельно упрощенной моделью таких систем. С учетом зазоров в передачах сухого и вязкого трения и кинематических погрешностей передач система уравнений движения механической части привода (2.2) может быть записана в следующем общем виде:

, (2.9)

где M₁₂ = c₁₂(₁ – ₂ – _к.п. – _3/2) – момент нагрузки в упругой связи с учетом зазоров в передачах _к.п. при /₁ – ₂ – _к.п./ > _3/2 и M₁₂ = 0 при /₁ – ₂ – _к.п./ < _3/2;

- момент нагрузки упругой связи с учетом момента потерь на внутреннее вязкое трение ;

- момент нагрузки упругой связи с учетом направления потоков энергии через передачи электропривода, т.е. учета влияния динамических нагрузок на механические потери; - переменная, составляющая момента потерь, пропорциональная моменту нагрузки передачи; - к.п.д. передачи; М₀ – постоянная составляющая момента потерь; и – активные постоянные моменты нагрузки на соответствующих валах; и - моменты сухого трения на соответствующих валах; и - моменты вязкого сухого трения на соответствующих валах.

Приведение зазоров осуществляется по следующим правилам:

для элемента с вращательным движением и угловым зазором ^­_3j, рад, приведенное значение зазора ^­_3k = ^­_3j;

для элемента с поступательным движением и линейным зазором ^­_3i, м приведенное значение зазора ^­_{3 л} = ^­_3i/p.

В реальных системах неограниченного возрастания амплитуд колебаний не наблюдается, так как этому препятствуют силы вязкого трения, поглощающие энергию механических колебаний. Силы внутреннего вязкого трения возникают при деформации механического оборудования и поэтому они пропорциональны скорости деформации элемента и направлены противоположно скорости деформации:

М_в.т. = ₁₂ (_i1 – _i2), (2.10)

где _i1, _i2 – угловые скорости концов деформируемого элемента. Внутреннее вязкое трение, не меняя общей формы и фазы колебаний, вызывает затухание колебаний и некоторое уменьшение частоты.

Обобщенная структурная схема механической части электропривода, соответствующая системе (2.9), приведена на рис. 2.2.

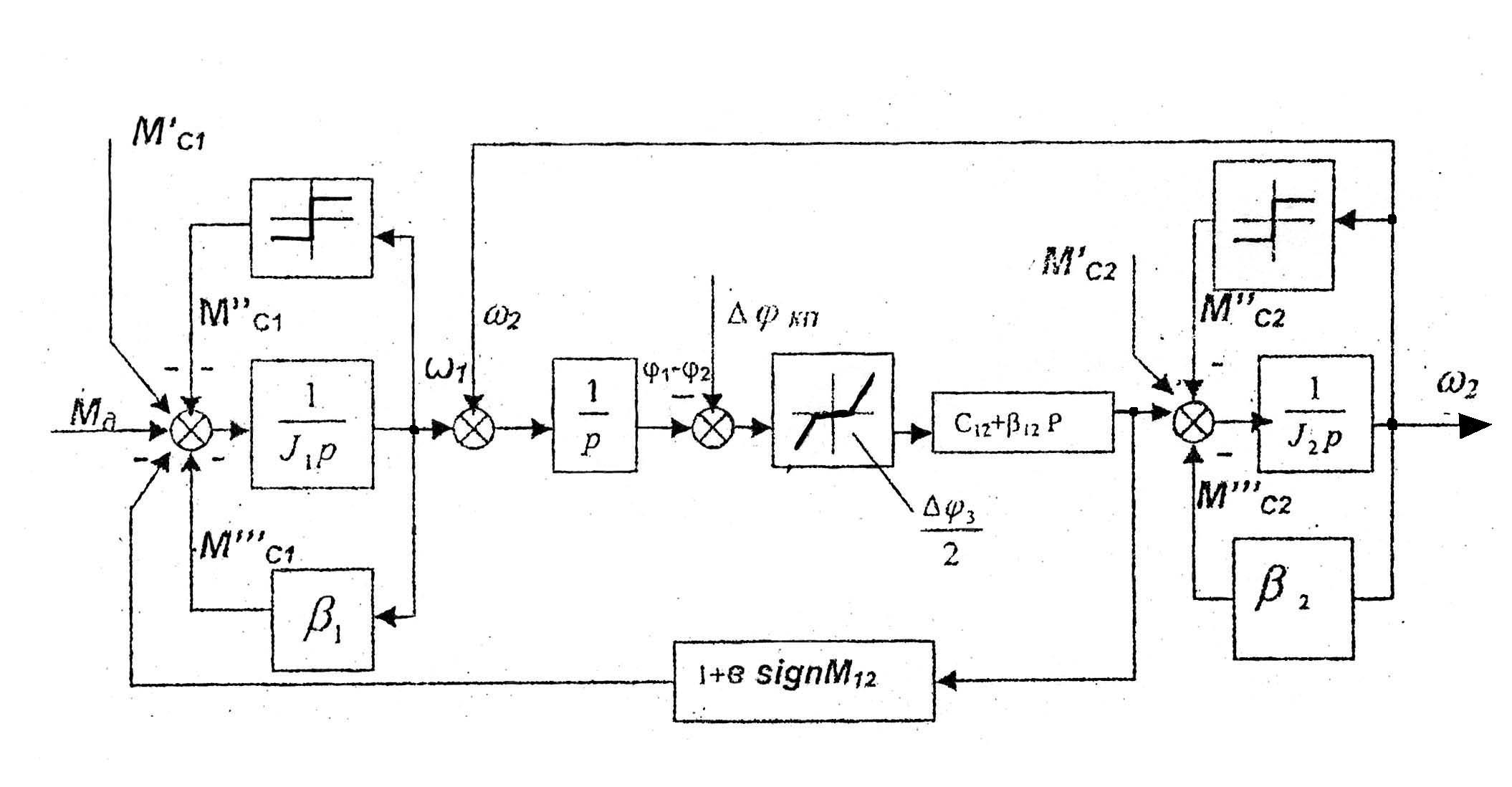
Рис. 2.2 Обобщенная структурная схема механической части электропривода

По этой схеме видно, что механическая часть электропривода представляет собой объект управления с существенными нелинейностями, обусловленными наличием зазоров, сухого и вязкого трения. Чаще всего при исследованиях электропривода не возникает необходимости в одновременном учете всех факторов и нелинейностей.