Числовая последовательность

Числовая последовательность — это последовательность элементов числового пространства.

Операции над последовательностями

На множестве всех последовательностей элементов множества   можно определить арифметические и другие операции, если таковые определены на множестве  . Такие операции обычно определяют естественным образом, т. е. поэлементно.

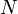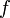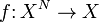
Пусть на множестве   определена  -арная операция  : Тогда для элементов 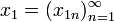 ,  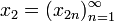, …,   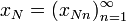множества всех последовательностей элементов множества   операция  будет определяться следующим образом: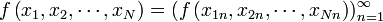

Например, так определяются арифметические операции для числовых последовательностей.

Суммой числовых последовательностей   и   называется числовая последовательность   такая, что  .

Разностью числовых последовательностей   и   называется числовая последовательность   такая, что  .

Произведением числовых последовательностей   и   называется числовая последовательность   такая, что  .

Частным числовой последовательности   и числовой последовательности  , все элементы которой отличны от нуля, называется числовая последовательность 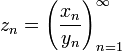 . Если в последовательности   на позиции   всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность  .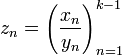

Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.

Предел последовательности

Основная статья: Предел последовательности

Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.

Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.

Верхний предел последовательности — это наибольшая предельная точка этой последовательности.

Нижний предел последовательности — это наименьшая предельная точка этой последовательности.

 Теоремы о пределах

1. Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение d > 0, что для всех x удовлетворяющих неравенству |x-a| < dимеет место неравенство |f(x)| > M.

lim_x® a=Ґ

2. Функция ограниченная при x® a.

3. Функция ограниченная при x® Ґ.

4. Теорема. Если lim_x® a f(x)=b, то функция f(x) ограниченная при x® a.

5. Бесконечно малые и их свойства. lim_x® a a(x)=0

Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то lim_x® a f(x)=b и обратно, если lim_x® af(x)=b, то можно записать f(x)=b+a(x).

Теорема. 2. Если lim_x® a a(x)=0 и a(x) № 0, то 1/a® Ґ.

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

6. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x) Ј z(x) Ј v(x), и lim_x® a u(x)=lim_x® a v(x)=b, то lim_x® a z(x)=b. ("Теорема о двух милиционерах").

Первый замечательный предел

 (второй замечательный предел).