
- •5. Дешифраторы.
- •8. Сумматоры
- •9. Вычитатели.
- •10. Цифровые компараторы
- •11. Перемножители
- •15. Счётчики.
- •16. Реверсивные счётчики.
- •17. Разновидности регистров. Параллельные регистры.
- •18. Сдвиговые регистры.
- •19. Реверсивные регистры.
- •20. Запоминающие устройства. Разновидности, характеристики.
- •21. Структуры зу.
- •23. Пзу и ппзу.
- •26. Плис. Общие понятия. Разновидности.
- •27. Программируемые логические матрицы (pla).
- •28. Программируемая матричная логика (pal), базовые матричные кристаллы (ga).
- •29. Программируемые вентильные матрицы (fpga). Программируемые коммутируемые матричные блоки (cpld)
- •31. Плис типа «система на кристалле (SoC).
- •32. Цап. Общие положения. Погрешности цап.
- •33. Цап с суммирование токов.
- •34. Цап типа r-2r.
- •40. Конвейерные ацп.
- •35. Сегментированные цап.
- •36. Цифровые потенциометры. Цап прямого цифрового синтеза.
- •37. Ацп. Общие положения. Параметры ацп. Погрешности ацп.
- •38. Разновидности ацп. Параллельные ацп.
- •39. Ацп поразрядного уравновешивания.
35. Сегментированные цап.
На практике на выходе наблюдаются выбросы, амплитуда которых зависит от номера переключаемого разряда.
Д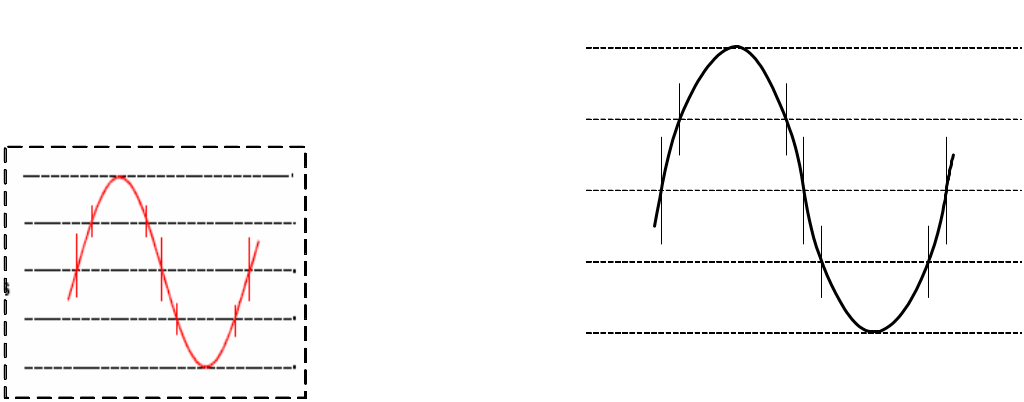 ля
устранения этих недостатков применяются
сегментированные ЦАП, в которых
используются два вида преобразователей:
ЦАП с суммированием токов (суммированием
весовых токов, матрицей R-2R,
с внутренними источниками тока) и
простейшие строковые ЦАП с выходом по
току или по напряжению
ля
устранения этих недостатков применяются
сегментированные ЦАП, в которых
используются два вида преобразователей:
ЦАП с суммированием токов (суммированием
весовых токов, матрицей R-2R,
с внутренними источниками тока) и
простейшие строковые ЦАП с выходом по
току или по напряжению
Принцип построения сегментированных ЦАП заключается в том, чтобы старшие разряды, дающие наибольшие погрешности, отделить от младших и преобразовать их в аналог с помощью строкового ЦАП, дающего малые кодозависимые помехи, младшие разряды преобразовать в аналог с помощью обычной двоичной схемы ЦАП, а на выходе произвести суммирование двух выходных сигналов, соответствующих младшим и старшим разрядам.
Функциональная схема сегментированного 10-ти разрядного ЦАП
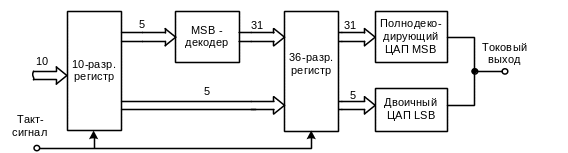 Входной
10-ти разрядный регистр предназначен
для ввода и хранения входного двоичного
параллельного кода. Дешифратор преобразует
пять старших разрядов входного
параллельного кода в позиционный
31-разрядный код. Таким образом второй
36-ти разрядный регистр хранит 31-ти
разрядный позиционный код старших
разрядов и пятиразрядный параллельный
двоичный код пяти младших разрядов.
Этот регистр необходим из-за задержки
прохождения сигналов через дешифратор.
Позиционный код поступает на строковый
ЦАП, младшие пять разрядов – на двоичный
ЦАП с параллельным входным кодом, как
правило, с суммированием токов и с
матрицей R-2R.
На выходе токи этих двух ЦАП суммируются.
Входной
10-ти разрядный регистр предназначен
для ввода и хранения входного двоичного
параллельного кода. Дешифратор преобразует
пять старших разрядов входного
параллельного кода в позиционный
31-разрядный код. Таким образом второй
36-ти разрядный регистр хранит 31-ти
разрядный позиционный код старших
разрядов и пятиразрядный параллельный
двоичный код пяти младших разрядов.
Этот регистр необходим из-за задержки
прохождения сигналов через дешифратор.
Позиционный код поступает на строковый
ЦАП, младшие пять разрядов – на двоичный
ЦАП с параллельным входным кодом, как
правило, с суммированием токов и с
матрицей R-2R.
На выходе токи этих двух ЦАП суммируются.
36. Цифровые потенциометры. Цап прямого цифрового синтеза.
Основу цифровых потенциометров составляет резистивная матрица, как правило, из 256 резисторов равного сопротивления, соединенных последовательно (рис.28.12). Вывод С через ключи S0…S255 может подключаться к любой точке резистивной цепи в зависимости от входного кода. Входной двоичный код преобразуется дешифратором 8×256 в позиционный код, управляемый ключами.
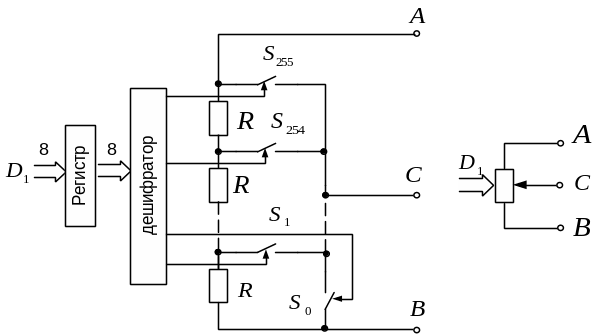
а) б)
Существует большое количество моделей цифровых потенциометров – без энергонезависимой памяти, с однократным программированием, с энергозависимой памятью. Энергонезависимое ЗУ особенно удобно для построения схем с автоматической подстройкой.
Основными областями применения цифровых потенциометров являются перестраиваемые фильтры, линии задержки, времязадающие цепи; схемы перестройки коэффициента передачи, усиления, уровня; согласование импедансов и замена механических потенциометров.
37. Ацп. Общие положения. Параметры ацп. Погрешности ацп.
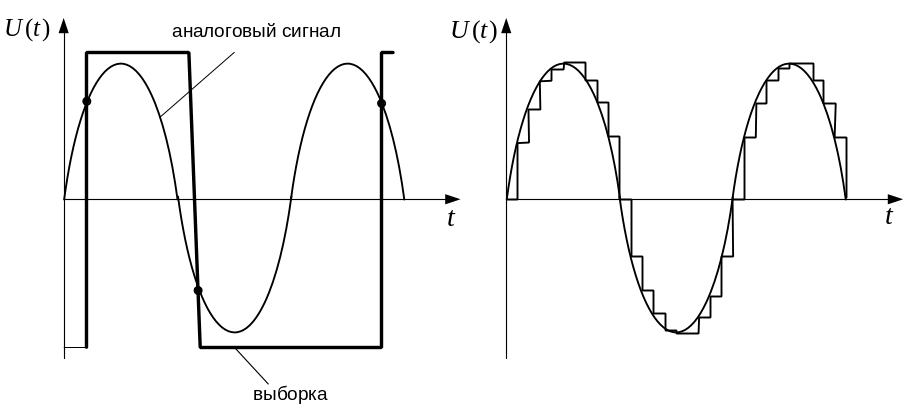
Процедура аналого-цифрового преобраз. непрерывного сигнала представ. собой преобраз. Непрерыв. ф-ции U(t) в послед-сть чисел U(tn), где n = 0, 1, 2 …, отнесенных к некоторым фиксир. моментам t. При дискрет-ции непрерыв. ф-ция U(t) преобраз-ся в послед-ть ее отсчетов U(tn), как показано на рис.28.1, а.

Рис.29.1. Процесс дискретизации (а) и квантования (б) непрерывного сигнала.
Квантование: мгновенные знач. Ф-ции u(t) ограничиваются только опр. уровнями, кот. наз. уровнями квантования. В рез-те квантования непрерывная ф-ция U(t) принимает вид ступенчатой кривой UК(t), показанной на рис.29.2,б.
Кодирование представл. дискретные квантованные вел-ны в виде цифрового кода. С помощ. операции кодирования осущ. условное представл. численного зн-ия вел-ны.
Чем меньше интервал дискрет-ции, тем точнее представляется сигнал. При малом интервале дискрет-ции необходим большой объем памяти и высокое быстродействие АЦП..
Частоту взятия выборок fВ опр. из т. Котельникова: fВ ≥ 2fМАКС,где fМАКС – наиб. частота спектра дискретизируемого сигнала.
а) б)
Рис.29.2. Неправильный (а) и правильный (б) выбор интервала дискретизации
При дискрет-ции возникает погрешность, обусловленная конечным временем одного преобраз-ния и неопределен. момента t его окончания. При равномерной дискрет-ции отсчеты берутся с периодом ТВ, однако в эти моменты только нач-ся процесс преобраз-я. Окончание этого процесса зависит от t преобразования АЦП и скорости изменения вх-ой вел-ны. В рез-те вместо равномерной дискрет-ции получ-ся дискрет-ция с перемен. периодом. Погрешность наз-ся апертурной. tА - время, в течение кот. сохр-ся неопр. м/у значением выборки и t, к которому она относится (рис.29.4).
Апертурная погрешность: δА = ΔuА / Uмакс = ω tА. T / tА = π / δА.. Для ↓ апертурной погрешности приходится в π / δА ↑ частоту преобразю АЦП.
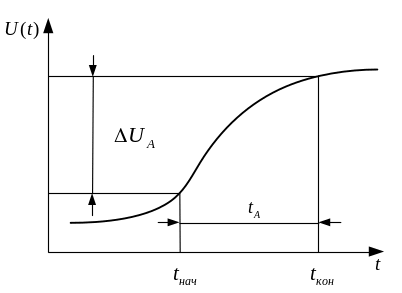
Рис.29.4. Апертурная погрешность
Цифровое представление
сигнала всегда дискретно, число его
возможных сост. опр-ся разреш. способностью,
т.е. разрядностью АЦП. Разность м/у 2я
соседними знач-ми квантованной вел-ны
наз-ся шагом квантования h.
Любой аналоговый сигнал, поступающий
на вх. идеального N-разрядного
АЦП, производит шум квантования.
Среднеквадратическое зн. шума ≈ весу
h
/![]() .
.
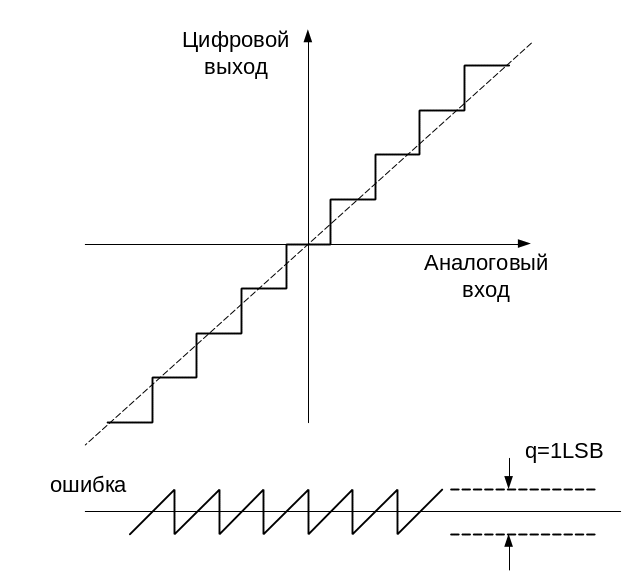
Рис.29.5. Хар-ка идеального квантователя (а) и погрешность квантования (б)
Параметры АЦП хар-ют преобразователь в статич., динамич. режимах, а также опр. погрешности квантования.
Погрешность квантования АЦП опр-ся соотношением сигнал/шум SNR.
Статич. параметры АЦП.
Динамич. параметры. Динамич. погрешности связаны с дискрет-цией сигналов, изменяющихся во времени.
1. Макс. частота дискрет-ции –наиб. частота, с кот. осущ. выборки вх-го сигнала при усл., что выбранный параметр не выходит за заданные пределы.
2. t преобразования – t, отсчитываемое от начала импульса дискрет-ции или начала преобраз-ия до появл. на вых-е устойчивого кода, соответ. данной выборке.
3. t выборки (стробирования) – t, в течение кот. происх. образ-ие одного выборочного значения.
