
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
Пусть
в задаче ОБ движение объекта подчиняется
системе (1) ДУ:
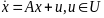 (1).
(1).
Т1:
Пусть
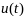 некоторое допустим управление,
- соотв решение системы(1), удовл гранич
условиям
некоторое допустим управление,
- соотв решение системы(1), удовл гранич
условиям
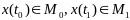 ;
;
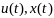 опред на отр
опред на отр
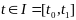 .
На отр времени
сущ решение вспомагат системы
.
На отр времени
сущ решение вспомагат системы
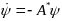 (2)
с нач условием
(2)
с нач условием
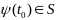 ,
где
,
где
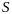 – сфера. Пара
– сфера. Пара
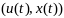 вместе с решением
системы(2) удовлетв след условиям:1.
усл максимума:
вместе с решением
системы(2) удовлетв след условиям:1.
усл максимума:
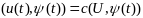 ,
,
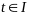 (3),
для почти всех
(за исключением меры мн-ва
(3),
для почти всех
(за исключением меры мн-ва
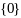 );
2.
усл трансверсальности на мн-ве
);
2.
усл трансверсальности на мн-ве
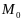 :
: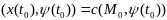 (4);
3.
усиленное усл трансверсальности на
мн-ве
(4);
3.
усиленное усл трансверсальности на
мн-ве
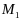 :
:
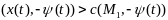 (5),
выполняется
(5),
выполняется
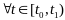 .Тогда
управление
оптимально. Док-во:
Пусть
.Тогда
управление
оптимально. Док-во:
Пусть
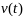 некоторое допустимое управление и
некоторое допустимое управление и
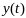 соотв ему решение системы (1) на отрезке
времени
соотв ему решение системы (1) на отрезке
времени
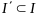 .
Определим ф-цию
.
Определим ф-цию
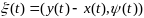 (6).
Покажем, что
(6).
Покажем, что
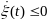 (7) для
почти всех
(7) для
почти всех
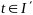 .
.
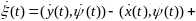
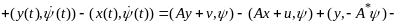
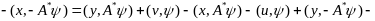
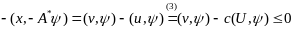 Нер-во (7) доказано. Предположим, что
выполн усл теоремы, но управлен
не явл оптим.; т.е. сущ управл
Нер-во (7) доказано. Предположим, что
выполн усл теоремы, но управлен
не явл оптим.; т.е. сущ управл
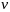 и соотв ему реш
,
кот переводит объект из мн-ва
на мн-во
,
при
и соотв ему реш
,
кот переводит объект из мн-ва
на мн-во
,
при
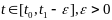 .
Рассм знач ф-и
.
Рассм знач ф-и
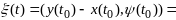
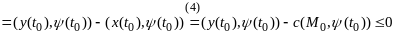 (8).
Ф-ция
(8).
Ф-ция
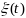 может быть представлена:
может быть представлена:
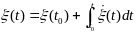 и из нер-в (8) и (7)
и из нер-в (8) и (7)
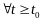 .
Рассмотрим значение
.
Рассмотрим значение
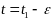 и скаляр произведение
и скаляр произведение
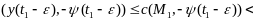 {из усл (5)}
{из усл (5)}
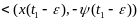 ,
тогда
,
тогда
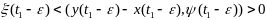 .
.
47. Пример решения задач оптимального быстродействия.
Пример
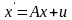 A=
A=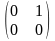 u=
u=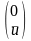
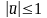
U={u
є R2|
u1=0,
|u2|
1}
M0
={x0}є
R2
, M1={0}
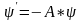
A*=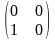
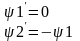
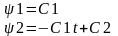 C1,С2-
const
C1,С2-
const
усл.
Max c(U,
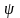 )=max(u,
)=max
u2
2
=|
2|
)=max(u,
)=max
u2
2
=|
2|
(u(t), (t))=| 2|, u2(t) 2(t) =| 2(t)|
1, 2>0
u2= [-1;1], 2(t)=0
-1, 2<0
2) усл. трансверсальности на M0
(x(t0), (t0))=C(M0, 2(t0))=(x0, (t0))
x(t0)=X0
3) усл. трансверсальности на M1
(x(t1), - (t1))=C(M1, - (t1))=0
x(t1)=0
I
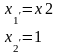
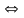
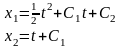
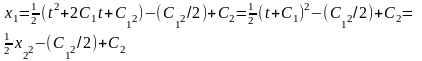
II
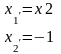
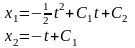
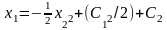
Усиленное
условие трансверсальности (x(t),
-
(t))>0
tє[0;t1)
Предположим, что начальная точка нах-ся
выше линии переключения управления.
Обозн. через
момент переключения уровня
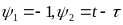
Рассмотрим
моменты времени
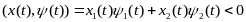 tє[
,t1)
tє[
,t1)
Т.к.
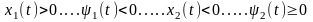
При tє[0; )
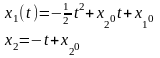
(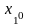 ;
;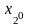 )=
- начальная
точка
)=
- начальная
точка
При
чем
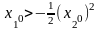
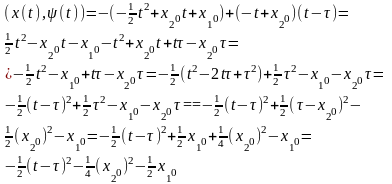
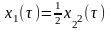
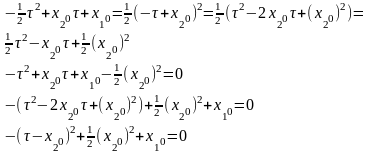
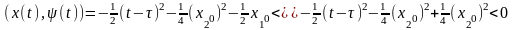
Если точка лежит ниже линии переключения, то рассуждения симметричны.
