44. Принципы динам програм и функцон ур-ния Беллмана.

В осн вычисл алгоритмов метода ДП лежит след принцип оптимальности: каково бы ни было состояние системы в рез 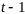шагов управление на шаге должно выбираться так, чтобы оно в совокупности с управлениями на всех посл шагах с 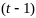до включительно, доставляло экстремум целев ф-ции.

Введем след обозначения: - мн-ва всех состояний в кот может нах система перед шагом . В частности при 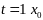-мн-во нач состояний; - мн-ыо управлений, ком могут быть выбраны на шаге и под воздейств каж их кот система переходит из сост принадлежащего мн-ву в сост, принадлежащее мн-ву ; 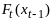- условно оптимальная значение цел ф-ции, если процесс рассм на инт от шага до шага при усл, что перед шагом система находилась в одном их сост мн-ва и на шаге было выбрано управление из мн-ва , которое обеспечило цел ф-ции усл оптим значения; 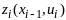- значение целевой ф-ции на ш–ом шаге для всех управлений их мн-ва 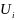при усл, что система нах-лась в одном их сост мн-ва 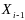. В принятых обозначениях принцип опт-ти можно записать в след форме:

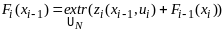(1)

Ур-ние (1) наз функцион ур-нием ДП(функц Ур Беллмана). Для последнего шага Ур (1) приним вид: 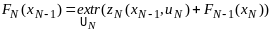, т.к. ф-ции опред для 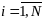, то 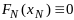. И тогда на посл шаге справ-во ур-ние: 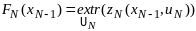(2).Т.к. рассм система без последействия, то 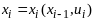(3), то на основании ур (1)-(3) с учетом конкрет мн-в 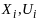строится высислительная процедура МДП, кот разделяется на 2 этапа: 1. условную; 2. безусловную оптимизацию.

Усл опт-ция осуществляется путем обратного движения от последнего шага к первому. Из ур (2) находится такое упраление из мн-ва 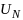, кот для каж состояния принадлежащего мн-ву 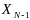доставляет экстремум ф-ции 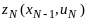и сисмема переходит в конечное состояние. Т.о для каждого состояния из мн-ва нах-ся условно-оптимальне знение целевй ф-ции и условно-оптим управление на последнем шаге. Далее из уравнения (1) нах-ся усл-оптим управление на 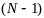шаге и усл-оптим значение целевой ф-ции на 2-ух последних шагах. При этом для каждого состояния из мн-ва 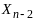и управления из мн-ва 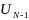по ф-ле (3) нах-ся соотв состояние из мн-ва и поэтому состоянию у учетом разультатов, предшествующих расчетов определяется усл-оатим значение целевой ф-ции, начиная у рассм шага до гонесного. Процесс продолжается до 1-го шага.

Безусл-оптим управление нах на этапе безусл оптимизации путем прямого движения от 1-го этапа к последнему.

Природа задачи, допускающая использование метода ДП не изменяется при изменении кол-ва шагов N. В этом смысле всякий конкрет процесс с задан кол-вом шагов оказывается как бы погруженным в сем-во подобных процессов и может рассм с позиции более широкого класса задач. В этом заключается 2-ой принцип ДП, наз-емый принципом погружения.

В силу этого св-ва при реш задачи методом ДП получают более широкий спектр рез-тов чем в исх постановке.

Заметим, что МДП при выборе решения на каж шаге учитывает интересы всего процесса, а не только интересы дан шага.

45. Постановка задачи оптимального быстродействия.

ЗОБ является частным случаем зад. оптим. управления при условии задания функционала кач-ва в виде

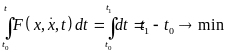
ЗОУ явл. обобщением в определенном смысле зад. вариационного исчисления когда мн-во кривых, среди которых опред. min функционала, явл. замкнутым.

Рассм. объект поведения к-рого описывается линейной системой ДУ

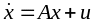, где , ,

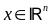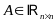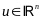
Пусть задано нек-рое непустое замкнутое и ограниченное мн-во U в пр-ве 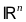. Вектор x будем наз. вектором фазового состояния объекта, а вектор u- вектором управления. Ф-ция u(t) наз. допустимым управлением на отр. 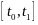, если она кусочно-непрерывна на этом отрезке и в каждый момент времени принимает значение из множества U. Подставляем различные допустимые управления в сист(1) будем получать соотв. этим управления решения x(t). Предложим , что дополнительно заданы 2 компактных мн-ва 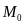и 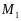. Говорят, что допустимое управление осуществляет переход из 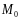в 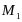, если соотв. Решение сист(1) удовл. условию:

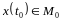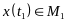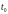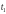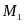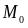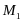, т.к. сист(1) явл. автономной, т.е. явно не зависящей от t, то момент времени можно считать фиксир. ,а момент времени определять из условия попадания на мн-во . Т.е. ЗОБ заключается в нахождении такого допустимого управления, переводящего объект из мн-ва в мн-во за наименьшее время.