3.3.2. Канонические и параметрические уравнения прямой

Положение прямой в пространстве должным образом определяется заданием т. .

Обозначим через (рис. 3.8).

Тогда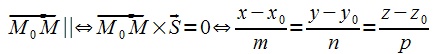 .Эти уравнения прямой именуют каноническими. Если приравнять эти отношения параметру и определить , то будем иметь параметрические уравнения прямой:

(3.3)

В евклидовом пространстве c ортонормированным базисом канонические уравнения прямой записываются как,

— направляющий вектор.

Допустим заданы две точки . В этом случае , получаем уравнения прямой, которая проходит через заданные точки: .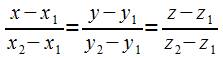

Например, уравнение прямой, которая проходит через две заданные точки ,  :

.

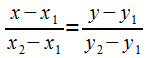3.3.3. Общие уравнения прямой

Проанализируем систему из двух уравнений I степени:

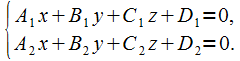(3.4)

Каждое из уравнений системы является определителем плоскости в пространстве, а вся система, при условии непараллельности плоскостей, — прямую, по которой они пересекаются. Эти уравнения именуют общими уравнениями прямой. Направляющий вектор подобной прямой определяется по формуле , где , — нормальные векторы плоскостей.

Задача. Даны общие уравнения прямой :

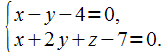
Вывести её канонические уравнения.

◄ Определяем направляющий вектор .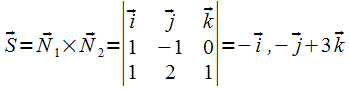

Для определения координат опорной т. , имеем систему для определения , :

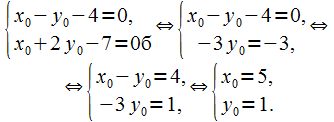
Следовательно, канонические уравнения прямой имеют следующий вид:

►

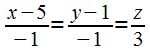3.3.4. Угол между двумя прямыми. Условия параллельности и перпендикулярности

Под углом между двумя прямыми в пространстве примем угол между их направляющими векторами и , то есть .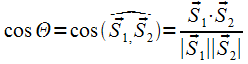

Условия параллельности и перпендикулярности прямых выводятся из условий параллельности векторов и : ; 

3.3.5. Угол между прямой и плоскостью

О: Углом между прямой и плоскостью именуется любой из двух смежных углов, который образован прямой и её проекцией на плоскость.

Пусть имеются направляющий вектор прямой и нормальный вектор плоскости . Тогда (рис. 3.9)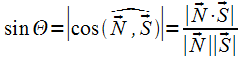

Условия параллельности и перпендикулярности записываются в виде ,  .

Линии второго порядка

Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек MЕвклидовой плоскости, для которых сумма расстояний до двух данных точек   и   (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

Свойства

• Оптические

  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.

  • Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

• Если   и   — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой 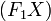  равен углу между этой касательной и прямой  .

• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяетпостроением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.

• Эволютой эллипса является астроида.

• Точки пересечения эллипса с осями являются его вершинами.

• Эксцентриситет эллипса равен отношению 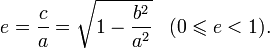 . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

• Эллипс также можно описать как

  • фигуру, которую можно получить из окружности, применяя аффинное преобразование

  • ортогональную проекцию окружности на плоскость.

  • Пересечение плоскости и кругового цилиндра

Гипе́рбола (др.-греч. ὑπερβολή, от др.-греч. βαλειν — «бросать», ὑπερ — «сверх») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек   и   (называемых фокусами) постоянно

Свойства

• Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

  • Иначе говоря, если   и   фокусы гиперболы, то касательная в любой точки 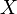  гиперболы является биссектрисой угла  .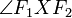

• Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

• Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.

• Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и bдруг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.

[править]Асимптоты

Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так какa = b = 1

Для гиперболы, заданной в каноническом виде

уравнения двух асимптот имеют вид:

.

Диаметры и хорды

Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент   параллельных хорд и угловой коэффициент   соответствующего диаметра связан соотношением

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы по её графику

[править]Касательная и нормаль

Поскольку гипербола является гладкой кривой, в каждой её точке (x₀, y₀) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

,

или, что то же самое,

.

Уравнение нормали к гиперболе имеет вид:

.

Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемойдиректрисой параболы) и данной точки (называемой фокусом параболы)

Свойства

• Парабола — кривая второго порядка.

• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.

• Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.

• Для параболы 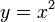  фокус находится в точке (0; 0.25).

Для параболы   фокус находится в точке (0; f).

• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

• Парабола является антиподерой прямой.

• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.