Векторы

Вектор в геометрии — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора. Операция сложения вводится по правилу треугольника: пусть есть векторы   и  . Оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Операция умножения вводится следующим образом: пусть есть вектор   и число  , тогда вектор   получается изменением длины вектора   в   раз. Направление вектора сохраняется, если   и меняется, если  .

Два геометрических вектора называются ортогональными, если они перпендикулярны друг другу.

Норма геометрического вектора определяется как длина соответвующего ему отрезка. Чаще всего называется модулем вектора и обозначается как  .

Определение скалярного произведения

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними

Свойства скалярного произведения

    1. Скалярное произведение обладает переместительным свойством: ab=ba

  

 Решение:                                                              

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b

.

 Векторным произведением векторов   и   называется вектор  , который определяется следующими условиями:

1) Его модуль равен   где   - угол между векторами   и  .

2) Вектор   перпендикулярен к плоскости, определяемой перемножаемыми векторами   и  .

Основные свойства векторного произведения:

1) Векторное произведение   равно нулю, если векторы   и   коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

Векторное произведение не обладает свойством переместительности.

Определения смешанного произведения, его геометрический смысл

Рассмотрим произведение векторов а, b и с, составленное следующим образом: (ахb )•с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Выясним геометрический смысл выражения (ахb )*с. Построим параллелепипед, ребрами которого являются векторы а, b , с и вектор d =ахb (см. рис. 22).

 

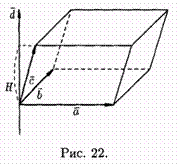
Имеем: (а х b) • с = d • с = |d| • пр_dс, |d|=|а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, пр_dс = Н Для правой тройки векторов и пр_dс = - Н для левой, где Н— высота параллелепипе­да. Получаем: (axb )*c =S *(±H ), т. е. (axb )*c =±V , где V — объем параллелепипеда, образованного векторами а, b и с.

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.