25. Расчет перемещений (прогибов) в жбк. Кривизна элементов.

Расчет перемещений железобетонных элементов — прогибов и углов поворота — связан с определением кривизны оси при изгибе или с определением жесткости элементов. По длине железобетонного элемента в зависимости от вида нагрузки и характера напряженного состояния могут быть участки без трещин (или участки, где трещины закрыты) и участки, где в растянутой зоне есть трещины. Считается, что элементы или участки элементов не имеют трещин в растянутой зоне, если при действии постоянных, длительных и кратковременных нагрузок с коэффициентом надежности по нагрузке трещины не образуются. Прогиб железобетонных элементов, не имеющих трещин в растянутых зонах определяют по жесткости приведенного сечения В с учетом значений коэффициента р при длительном действии нагрузки.

При определении перемещений железобетонных элементов постоянного сечения допускается на каждом участке, в пределах которого изгибающий момент не меняет знака, вычислять кривизну для наиболее напряженного сечения и далее принимать изменяющейся прямо пропорционально эпюре изгибающих моментов. Это допущение равносильно тому, что жесткость В вычисляют для наиболее напряженного сечения и далее принимают постоянной.

Для предварительно напряженных элементов, к которым предъявляются требования 2-й и 3-й категорий по трещиностойкости, такие допущения в ряде случаев приводят к существенному завышению прогиба против действительного значения, так как участки с трещинами в растянутой зоне могут иметь ограниченную протяженность. Прочность изгибаемых железобетонных элементов любого симметричного профиля по нормальным сечени­ям, согласно первой группе предельных состояний, рас­считывают по стадии III напряженного состояния. В расчетной схеме усилий принимают, что на элемент действует изгибающий момент М, вычисляемый при рас­четных значениях нагрузок, а в арматуре и бетоне дей­ствуют усилия, соответствующие напряжениям, равным расчетным сопротивлениям .

Схема усилий при расчете прочности изгибаемых элемен­тов по нормальному сечению. В бетоне сжатой зоны криволинейную эпюру напряжений заменяют (для упрощения) прямоугольной, что на значение момента влияет несущественно.

Сечение элемента может быть любой формы, симмет­ричной относительно оси, совпадающей с силовой плос­костью изгиба. В растянутой зоне сечения элемента в об­щем случае имеется арматура без предварительного напряжения площадью сечения A_sс расчетным сопротивлением растяжению R_s, а также предварительно напря­гаемая арматура площадью A_spи своим расчетным сопротивлением К_s. Рекомендуется применять изгибаемые элементы при сечениях, удовлетворяющие условию случая 1: x<E_Rh₀.

Равнодействующие нормальных напряжений в арма­туре и бетоне

N_S = R_SA_S; Np = y_s6R_sA_sP; N_b = R_bA_bc; N'_s = R_cA'_s; N'_sp = G_sCA'_sp.

При моментах, взятых относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через точ­ку приложения равнодействующей усилий во всей растя­нутой арматуре A_sи A_sp, условие прочности выражается неравенством,

M<R_bA_bc_zb+R_scA_s(ho-a)+G_scA_sp(ho-a)

Если в сечении отсутствуют отдельные виды растяну­той или сжатой арматуры, то выпадают и соответствую­щие члены в приведенных формулах.

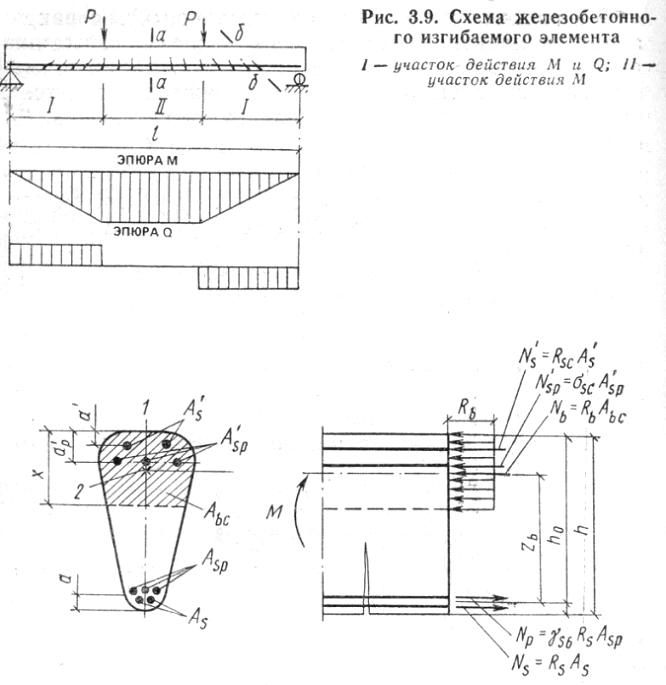
Рисунок 1 – Схема железобетонного изгибаемого элемента

1 — ось симметрии сечения элемента; 2 — центр тяжести площади бетона сжа­той зоны; а — расстояние от равнодействующей усилий в арматуре A_s и A_spдо растянутого края сечения (все остальные буквенные обозначения на ри­сунке — общепринятые) (рис. ).

К изгибаемым элементам относятся плиты (панели) и балки.

Плитами называют железобетонные элементы, в которых один размер (толщина h_f) значительно меньше двух других: пролета l_f и ширины поперечного сечения b_f.

Кривизну железобетонных элементов с трещинами и без трещин можно также определять на основе деформационной модели. Полную кривизну изгибаемых элементов определяют:

а) для участков без трещин в растянутой зоне по формуле

где - кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок;

- кривизна от непродолжительного действия усилия предварительного обжатия Р (т.е. при действии M = Pe_op)

б) для участков с трещинами в растянутой зоне по формуле

где  - кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям;

- кривизна от непродолжительного действия постоянных и длительных нагрузок;

- кривизна от продолжительного действия постоянных и длительных нагрузок.