
- •1) Определение матрицы. Виды матриц. Транспонирование матриц. Алгебраические операции над матрицами. Свойства алгебраических операций над матрицами. (из тетрадки моей читай!!!тут не так)
- •2) Определители второго, третьего порядков и матрицы n-го порядка. Свойства определителей.
- •3) Алгебраическое дополнение и его свойства. Разложение определителя по строке
- •4) Присоединенная и обратная матрицы. Критерий обратимости.
- •5)Ранг матрицы как наивысший порядок ее миноров, отличных от нуля. Вычисление ранга матрицы с помощью элементарных преобразований.
- •6)Система n линейных уравнений с n переменными (общий вид). Матричная форма записи системы. Совместные и несовместные, определенные и неопределенные системы
- •7)Теорема Крамера о разрешимости системы n линейных уравнений с n переменными.
- •8) Метод Гаусса решения систем линейных уравнений. (отсюда читай!!!и чуточку из моей)
- •9) Определение комплексного числа. Операции над комплексными числами.
- •10) Поле комплексных чисел
- •11) Тригонометрическая форма. Формула Муавра.
- •12) Извлечение корней из комплексного числа
- •13) Показательная форма записи комплексных чисел и ее свойства
- •14) Формулировка основной теоремы алгебры
- •15) Определение системы координат на плоскости и в пространстве (декартова и полярная системы координат). Преобразование декартовой системы координат. (половину у меня бери!!а начало от сюда!!)
- •23. Линии второго порядка на плоскости(окружность и эллипс-смотри 24 билет)
- •Элементарное определение
- •Связанные определения
- •Билет 31. Базис. Размерность(тут муть!!!если попадется на мути что-нибудь…)
Билет 31. Базис. Размерность(тут муть!!!если попадется на мути что-нибудь…)
Конечная сумма вида
![]()
называется линейной
комбинацией
элементов
![]() с
коэффициентами
с
коэффициентами
![]() .
.
Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.
Элементы
 называются
линейно
зависимыми,
если существует их нетривиальная
линейная комбинация, равная нулевому
элементу
называются
линейно
зависимыми,
если существует их нетривиальная
линейная комбинация, равная нулевому
элементу
 .
В противном случае эти элементы
называются линейно
независимыми.
.
В противном случае эти элементы
называются линейно
независимыми.Бесконечное подмножество векторов из называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.
Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меля или линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса:
Любые линейно независимых элементов -мерного пространства образуют базис этого пространства.
Любой вектор можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
![]() .
.
Базис пространства . Координаты вектора
Базис
- любая упорядоченная система
![]() из
n
линейно независимых векторов пространства
.
из
n
линейно независимых векторов пространства
.
Обозначение:
![]()
Для
каждого вектора
существуют
числа
![]() такие
что
такие
что
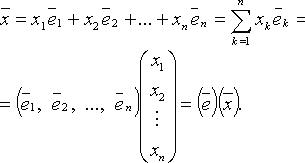
Числа
![]() называются
координатами вектора
в
базисе (
)
(определяются однозначно), X
= (x) -
координатный столбец вектора
в
этом базисе. Употребляется запись:
называются
координатами вектора
в
базисе (
)
(определяются однозначно), X
= (x) -
координатный столбец вектора
в
этом базисе. Употребляется запись:
![]()
Справедливы формулы:

Матрица системы векторов
Для
векторов
![]()
![]() ...,
...,
![]() в
базисе (
)
- матрица
в
базисе (
)
- матрица

m векторов пространства линейно независимы тогда и только тогда, когда rank A = m.
Матрица
S
перехода от базиса
![]() к
базису
к
базису
![]() -
матрица системы векторов
-
матрица системы векторов
![]() в
базисе
в
базисе
![]()
Если
 ,
то:
,
то:

или кратко:
![]()
Если
![]() то
то
![]() т.
е.
т.
е.
![]() -
матрица перехода от базиса
к
базису
.
-
матрица перехода от базиса
к
базису
.
Преобразование координат вектора
Если
![]() то
В
развернутой записи:
то
В
развернутой записи:
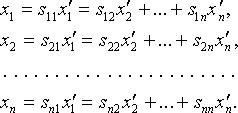
Очевидно, что
![]()
Пример.
Найдите
фундаментальную систему решений и общее
решение однородной системы линейных
алгебраических уравнений
 .
Решим
ее методом Крамера:
.
Решим
ее методом Крамера:
 Таким
образом,
Таким
образом,
 .
Теперь
построим X(2).
Для этого придадим свободным неизвестным
переменным значения x2
= 0, x4
= 1, тогда
основные неизвестные найдем из системы
линейных уравнений
.
Теперь
построим X(2).
Для этого придадим свободным неизвестным
переменным значения x2
= 0, x4
= 1, тогда
основные неизвестные найдем из системы
линейных уравнений
![]() .
Опять
воспользуемся методом Крамера:
.
Опять
воспользуемся методом Крамера:
 Получаем
Получаем
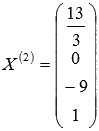 .
Так
мы получили два вектора фундаментальной
системы решений
и
,
теперь мы можем записать общее решение
однородной системы линейных алгебраических
уравнений:
.
Так
мы получили два вектора фундаментальной
системы решений
и
,
теперь мы можем записать общее решение
однородной системы линейных алгебраических
уравнений:
 ,
где C1
и C2
– произвольные числа.
,
где C1
и C2
– произвольные числа.
