15) Определение системы координат на плоскости и в пространстве (декартова и полярная системы координат). Преобразование декартовой системы координат. (половину у меня бери!!а начало от сюда!!)

Декартовой называют прямоугольную систему координат с одинаковыми масштабами по осям

Прямоугольная система координат - прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Билет 15. Декартовой системой координат в пространстве называется совокупность точки и базиса. Плоскости, проходящие через оси координат, называют координатными плоскостями. Декартова система координат называется прямоугольной, если векторы базиса -- единичные и попарно ортогональные (перпендикулярные) друг другу.      

Базис, образованный единичными попарно ортогональными векторами, называют ортонормированным.  Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е. 90 градусов.  Полярная система координат — (плоскость)двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов. Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку. Преобразование декартовой системы координат. Пару полярных координат и можно перевести в Декартовы координаты и путём применения тригонометрических функций синуса и косинуса:

в то время как две декартовы координаты и могут быть переведены в полярную координату :

(по теореме Пифагора).

Для определения угловой координаты следует принять во внимание два следующие соображения: 1). Для , может быть произвольным действительным числом.2). Для , чтобы получить уникальное значение , следует ограничиться интервалом в . Обычно выбирают интервал или .

Билет 16. Вектор – это направленный отрезок прямой. Нулевой вектор(0 и наверху вектор)– это любая точка плоскости или пространства. Длина вектора AB- это неотрицательное число, равное длине отрезка АВ. Длину вектора АВ будем обозначать как (модуль вектора АВ). Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Два вектора называют компланарными, если они лежат либо на одной плоскости , либо на параллельных плоскостях. Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых. Два коллинеарных вектора называют сонаправленными, если их направления совпадают и обозначают(а и 2 стрелочки наверх и б). Два коллинеарных вектора называют противоположно направленными, если их направления противоположны и обозначают(также а и 2 стрелочки наверх б). Два вектора называются равными, если они сонаправленные и их длины равны. Два вектора называются противоположными, если они противоположно направлены и их длины равны. Угол между сонаправленными векторами равен нулю градусам (или нулю радиан), а угол между противоположно направленными векторами равен 180 градусам (или радиан). Два вектора называются перпендикулярными, если угол между ними равен 90 градусам (или ПИ/2 радиан). Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

Проекция вектора на ось обозначается через a_l или , а угол между осью и вектором будем обозначать так: . Таким образом,   Если - углы, образованные вектором с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора на координатные оси будут равны

     (3) Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле

     (4) Вектор равен нулю, если все три его проекции равны нулю

Разложение вектора по ортам координатных осей. Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i , j , k соответственно (см. рис. 12).

 

Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ. Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М₁ , М₂ и Мз.Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр _ха=|OM ₁|, np_ya = |ОМ₂|, пр_z а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ ₁ + M₁N + NM.

А так как M ₁N=OM ₂ , NM =ОМз, то

а=ОМ ₁ + ОМ ₂ + ОМ₃                                             (5.1)

 

Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через а_х, а_у и a_z, т.е. |OM ₁| = а_х,|ОМ₂| = а_у, |ОМ₃| = а_z. Тогда из равенств (5.1) и (5.2) получаем

a=a_xi+a_yj+a_zk            (5.3)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_у, a_z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси. Билет 17. Линейные операции над векторами Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число. Пусть а и b — два произвольных вектора. Возьмем произвольную точку О и построим вектор ОА=а. От точки А отложим вектор АВ = b . Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b : О B=а+b. Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелoграмма (см. рис. 3).

На рисунке 4 показано сложение трех векторов а, b и с.

  Под разностью векторов а и b понимается вектор с=а-b такой, что b+с=а (см. рис. 5).

  Отметим, что в параллелограмме, построенном на векторах а и b одна направленная диагональ является суммой векторов а и b , а другая — разностью (см. рис. 6).

Можно вычитать векторы по правилу: а - b = а + (-b ), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным вектору b . Произведением вектора а на скаляр (число) λ  называется вектор λ*а (или а*λ), который имеет длину    |λ|*|а|, коллинеарен вектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0. Из определения произведения вектора на число следуют свойства этого произведения: 1) если b=λ * а , то b || а . Наоборот, если b ||а , (а0 ), то при некотором λ  верно равенство b = λа ; 2)    всегда а =|а | • а ^-о , т. е. каждый вектор равен произведению его мо дуля на орт.

Линейные операции над векторами обладают следующими свойствами: 1.    а+b=b+а 2.     (а +b) +с=а + (b +с), 3.    λ1 • (λ2 •а) =λ1 •λ2 •а, 4.      (λ1 +λ2) •а =λ1 •а +λ2 •а, 5.    λ • (а +b) =λ •а+λ •b. Билет 18. Углом ФИ между векторами a , b называется угол между векторами, равными данным и имеющими общее начало. Если не указано, от какого вектора и в каком направлении угол отсчитывается, то углом между векторами считается тот из углов, который не превосходит π . Если угол прямой, то векторы называются ортогональными. Если базис ортонормированный, то скалярное произведение векторов выражается через их компоненты a ={a₁;a₂;a₃},  b = {b₁;b₂;b₃} по формуле a⋅b =a₁b₁+a₂b₂+a₃b₃ . Скалярным произведением векторов a, b называется число a⋅b или (a,b ), равное произведению длин векторов на косинус угла между ними: Свойства скалярного произведения: 1. a⋅b=b⋅a ; 2. a⋅b=0 тогда и только тогда, когда векторы ортогональны; 3. Для любых чисел α,β и векторов a,b,c имеет место соотношение: (αa+βb)⋅c=α(a⋅c)+β(b⋅c) (линейность скалярного произведения); 4. a⋅a=|a|² . Векторным произведением векторов a,b называется вектор c , удовлетворяющий условиям: 1. c =a⋅b sinϕ , где ϕ есть величина угла между векторами. 2. Вектор c перпендикулярен векторам a,b . 3. Векторы a,b , c образуют правую тройку, т. е. из конца вектора c кратчайший поворот от вектора a к вектору b виден против часовой стрелки. Обозначается: c = a×b или c=[a,b ]. Геометрическое приложение векторного произведения. Из определения вытекает, что модуль векторного произведения неколлинеарных векторов численно равен площади параллелограмма, построенного на сомножителях Свойства векторного произведения: 1.  тогда и только тогда, когда векторы коллинеарны; в частности, [a,a] = 0 ; 2. (антикоммутативность векторного произведения); 3.  (линейность векторного произведения). Смешанным произведением векторов  называется число, равное скалярному произведению вектора a на вектор [b ,c] . Обозначается:  или . Геометрический смысл смешанного произведения. Модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах  как на сторонах  Если векторы образуют правую тройку, то смешанное произведение  > 0 ; если левую, то  < 0. Свойства смешанного произведения: 1.   (антикоммутативность смешанного произведения); 2.  (линейность смешанного произведения); 3.  тогда и только тогда, когда векторы компланарные.

Билет 19. Общее уравнение прямой Общее уравнение прямой линии на плоскости в декартовых координатах:

где , и  — произвольные постоянные, причем постоянные и не равны нулю одновременно. Вектор с координатами называется нормальным вектором, он перпендикулярен прямой. Вектор с координатами (−B, A) или (B, −A) называется направляющим вектором. При прямая проходит через начало координат. Также уравнение можно переписать в виде

Уравнение прямой с угловым коэффициентом Уравнение прямой линии, пересекающей ось в точке и образующей угол с положительным направлением оси :

Коэффициент называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси

Получение уравнения прямой в отрезках

Получение уравнения прямой в отрезках Параметрические уравнения прямой

где  — производный параметр,  — координаты и направляющего вектора прямой. При этом

Каноническое уравнение прямой

где  — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.

Билет 20. Плоскость в пространстве. Получим сначала уравнение плоскости, проходящей через точку М₀(х₀ ,у₀ ,z₀) перпендикулярно вектору n = {A,B,C},называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор М₀М = {x - x₀ , y - y_{0 ,} z - z₀) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:

A(x - x₀) + B(y - y₀) + C(z - z₀) = 0. (8.1)

Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. После приведения подобных можно записать уравнение (8.1) в виде:

Ax + By + Cz + D = 0, (8.2)

где D = -Ax₀ - By₀ - Cz₀. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.

 Неполные уравнения плоскости.

Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение называют неполным.

Рассмотрим возможные виды неполных уравнений:

1)       С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz. 2)       А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу). 3)       А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz. 4)       B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz.5)       А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох. 6)       B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу. 7).     C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.

Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду:

называемому уравнением плоскости в отрезках

Параметрическое уравнение плоскости в координатной форме, в системе координат Oxyz

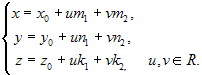                  (5.3.4)

Билет  21. Каноническое, параметрическое и общее уравнение прямой в пространств

Параметрическое уравнение прямой линии

  Векторное уравнение в координатной форме представляется следующим образом

(13.3)

Каноническое уравнение прямой линии в пространстве

  Исключив t из уравнения , разрешив их сначала относительно t, а затем, приравняв правые части равенств, имеем:

(13.4)

Если какая – либо координата направляющего вектора равна нулю, то равен нулю и числитель дроби.

Общее уравнение прямой линии в пространстве

  Прямая в пространстве может быть задана также как пересечение двух плоскостей, если плоскости не параллельны:

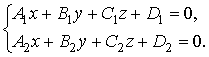
Все формы задания прямой в пространстве взаимосвязаны.

Билет 22. Расстояние от точки до плоскости, до прямой

 Расстояние от точки до плоскости

Пусть плоскость задана уравнением и дана точка . Тогда расстояние от точки до плоскости определяется по формуле

(11.7)

      

Расстояние от точки до прямой