
- •Вопрос 6 - Влияние вращения Земли на механические явления
- •Вопрос 8 - коэффициенты пропорциональности в формулах физики и размерности физических величин
- •Вопрос 10- Кинетическая Энергия
- •Вопрос 13. Потенциальные кривые. Равновесие.
- •Кинетическая энергия вращения
- •21. Момент импульса
- •22. Свободные оси вращения
- •23. Гидроскопы
- •24. Малые отклонения от равновесия
- •25. Частные случаи колебаний
- •Билет 38. Принцип Гюйгенса — Френеля. Отражение и преломление волн
- •Билет 40. Явление Доплера
- •Билет 41. Наложение двух волн, бегущих в противоположные стороны
- •Билет 42. Собственные колебания стержней
- •Билет 43. Собственные колебания двумерных и трехмерных систем
- •Билет 44. Вынужденные колебания стержней и пластинок
- •Билет 45. Колебания пьезоэлектриков
Вопрос 8 - коэффициенты пропорциональности в формулах физики и размерности физических величин
Коэффициент 7, входящий в закон всемирного тяготения, является универсальной постоянной, зависящей от выбора единиц измерения силы, массы и расстояния. Можно выбрать единицы измерения и так, чтобы было у= 1. Для этого за единицу массы надо принять массу точки, притягивающуюся к другой такой же, находящейся на единичном расстоянии, с единичной силой. В системе СГС такая масса равнялась бы, очевидно, 1,5-107 г, т. е. 15 тоннам
Важно усвоить следующее: применяемая система единиц измерения и коэффициенты пропорциональности в формулах связаны друг с другом. Эту связь можно обнаружить при рассмотрении формул размерностей. Прежде всего, необходимо установить число единиц, которые мы желаем считать основными. Это число целиком зависит от нашего произвола и определяется исключительно соображениями удобства
В физике общепринята система, в которой единицы измерения длины L, массы М и времени Т выбраны независимо друг от друга.
Тогда значения всех универсальных констант, а также единицы измерения всех других величин однозначно определяется выбором единиц для L, М и Т.
Таким образом, универсальные коэффициенты, фигурирующие в законах физики, появляются вследствие конкретного выбора единиц измерения. При желании можно было бы изгнать все коэффициенты этого рода из всех законов, выбирая соответствующим образом единицы измерения
Две популярные системы:
Система СГС: L - сантиметр, М - грамм, Т - секунда;
Система СИ: L - метр, М - килограмм, Т - секунда.
Вопрос 9 – Работа Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы. Движение без ускорения (т. е. прямолинейное и равномерное) может происходить как без действия, так и при действии на тело сил. В последнем случае сумма сил, действующих на тело, равна нулю. Между этими двумя видами движений без ускорения имеется существенное различие. В первом случае движение не сопровождается работой, для осуществления второго типа движения нужно затратить работу. Работает мотор, движущий равномерно и прямолинейно автомашину.
Вопрос 10- Кинетическая Энергия


Предыдущее уравнение читается теперь так: работа результирующей силы, действующей на тело (т. е. произведение тангенциальной составляющей результирующей силы на путь), равна приращению кинетической энергии тела. Это уравнение удобно для решения элементарных механических задач, в которых задан путь, на котором действовала сила.
Билет 11 потенциальная энергия Потенциальная энергия - энергия взаимодействия тел или частей тела.Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними. |
|
Потенциальная энергия тела, поднятого над Землей. Работа силы тяжести. |
|
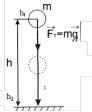
Пусть тело свободно падает с высоты h1 над уровнем Земли на уровень h2.
Тогда:
При падении сила тяжести совершает положительную работу, при движении тела вверх - отрицательную. Величину Eз = mgh называют потенциальной энергией взаимодействия тела и Земли. |
|
Т.о. A = - (Ep2 - Ep1) = -DEp Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот. |
Eз = mgh
A = - (Ep2 - Ep1) = -DEp |
Т.к. потенциальная энергия определяется координатой, то величина потенциальной энергии определяется выбором системы координат (выбором нулевого уровня). Т.е. она определяется с точностью до постоянной величины. В данной задаче удобно за точку отсчета выбирать уровень Земли. |
|
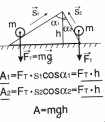
Если тело движется под углом к направлению вектора силы тяжести, то, как видно из рисунка, работа силы тяжести независимо от траектории определяется изменением положения тела (на рис. - высотой наклонной плоскости h). Если тело движется по произвольной траектории, то ее можно представить в виде суммы горизонтальных участков, на которых работа силы тяжести равна нулю, и вертикальных, на которых суммарная работа будет равна А=mgh. Работа силы тяжести не зависит от формы траектории и определяется только начальным и конечным положением тела. На замкнутой траектории работа силы тяжести равна нулю, т.к. потенциальная энергия не меняется. |
|
Потенциальная энергия тел, взаимодействующих посредством гравитационных сил. |
|
где r- расстояние между взаимодействующими телами. Знак "-" говорит о том, что это энергия притягивающихся тел. При сближении тел потенциальная энергия увеличивается по модулю. Работа по сближению двух астрономических объектов:
|
|
Потенциальная энергия упруго деформированного тела. Работа силы упругости. |
|
Для вывода формулы используем, что работа численной равна площади под графиком зависимости силы от координаты. При малых упругих деформациях сила упругости прямо пропорциональна абсолютной деформации (з-н Гука) - см. рис.
Тогда
работа при изменении деформации
от х1 до
х2 равна:
|
|
Учитывая з-н Гука,
получим:
|
|
Т.о.,
если принять за потенциальную энергию
упруго деформированного тела величину
где k -
коэффициент жесткости, а х -
абсолютная деформация тела, то можно
сделать вывод , что
т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком. |
|
Работа силы упругости зависит только от координат (начальной и конечной деформаций) тела и, следовательно, не зависит от траектории. Работа по замкнутой траектории равна нулю. |
|
Консервативные силы. Консервативными (сохраняющими) наз. силы, работа которых не зависит от траектории и по замкнутой траектории равна нулю (эти силы не зависят от скоростей). Примеры: гравитационные, упругие. |
|
Диссипативные силы Диссипативными (рассеивающими) наз. силы, работа которых зависит от траектории и по замкнутой траектории не равна нулю (такие силы зависят от скорости). Пример: сила трения. |
|
Билет 12 Закон сохранения механической энергии
Если в замкнутой системе не действуют силы, трения и силы сопротивления, то сумма кинетической и потенциальной энергии всех тел системы остается величиной постоянной.
Пример проявления этого закона. Пусть тело, поднятое над Землей, обладает потенциальной энергией Е1 = mgh1 и скоростью v1 направленной вниз. В результате свободного падения тело переместилось в точку с высотой h2 (E2 = mgh2), при этом скорость его возросла от v1 до v2. Следовательно, его кинетическая энергия возросла от

Запишем уравнение кинематики:

Умножим обе части равенства на mg, получим:

После преобразования получим:

Рассмотрим ограничения, которые были сформулированы в законе сохранения полной механической энергии.
Что же происходит с механической энергией, если в системе действует сила трения?
В реальных процессах, где действуют силы трения, наблюдается отклонение от закона сохранения механической энергии. Например, при падении тела на Землю сначала кинетическая энергия тела возрастает, поскольку увеличивается скорость. Возрастает и сила сопротивления, которая увеличивается с возрастанием скорости. Со временем она будет компенсировать силу тяжести, и в дальнейшем при уменьшении потенциальной энергии относительно Земли кинетическая энергия не возрастает.
Это явление выходит за рамки механики, поскольку работа сил сопротивления приводит к изменению температуры тела. Нагревание тел при действии трения легко обнаружить, потерев ладони друг о друга.
Таким образом, в механике закон сохранения энергии имеет довольно жесткие границы.
Изменение тепловой (или внутренней) энергии возникает в результате работы сил трения или сопротивления. Оно равно изменению механической энергии. Таким образом, сумма полной энергии тел при взаимодействии есть величина постоянная (с учетом преобразования механической энергии во внутреннюю).
Энергия измеряется в тех же единицах, что и работа. В итоге отметим, что изменить механическую энергию можно только одним способом - совершить работу.


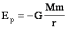 ,
, .
.
 .
.


 ,
, ,
,