5. Понятие тензора

Тензор – то, что отвечает трем пунктам:

1) это математическое представление некоторого объекта (геометрического или физического), существующего в пространстве, в виде таблицы величин – компонент тензора;

2) значения компонент тензора зависят от принятой системы координат и изменяются

(преобразуются) при переходе к другим координатам;

3) преобразование компонент таково, что оставляет, тем не менее, неизменными некоторые особые величины – инварианты(не зависят от выбора системы координат).

Классификация тензоров:

1.Тензоры, ранг которых 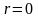являются скалярами. В связи с этим поле тензоров нулевого ранга называют скалярным полем.

2.Тензоры первого ранга – векторы – образуют векторные поля.

3. Для задания поля тензора ранга каждой точке М области G необходимо поставить в соответствие тензор второго ранга(матрица 3*3).

Ранг тензора- число элементов матриц прямого, обатного преобразований в законе преобразования его компонент.(на практике ранг считают по числу свободных индексов.)

Тензором ранга r в n-мерном пространстве называют математический объект с числом компонент N=n^r инвариантных относительно НОП, компоненты которого при этих преобразованиях изменяются по закону:

T^{’ m…s}_ijk.=(альфа)α^x_i α^y_j … α^z_k *β_l^m β_f^s *T_xyz^l...f

4. Тензор, компоненты которого удовлетворяют условию Тik= Тki, называется симметричным. Если компоненты обладают свойством Тik= -Тki, то тензор называется антисимметричным.

В случае тензора n-го ранга можно говорить о симметрии или антисимметрии его компонент относительно определенной пары индексов.

Тензоры, построенные по правилу прямого произведения называются мультипликативными или полиадными.

Теорема: всякий тензор представим в виде суммы мультиликативных тензоров соответствующего ранга и строения.

Обобщение законов преобразования:

ϕ^’=ϕ a^’ =a

a {a¹,a², a³} {a₁,a₂,a₃} b{b¹,b²,b³}{b₁,b₂,b₃}

прямое произведение: под прямым произведением множества А на множество В понимают множество С, элементами которого являются все упорядоченные пары, состоящие из одного элемента множества А и одного элемента множества В.

6.Единичный тензор

Полезным понятием является единичный тензор, обозначаемый символом Кронекера δ_i^k

Он определяется так: δ_i^kxⁱ= x^k (1.8)

– для любого вектора х. Единичный тензор как бы выделяет желаемую (k-ю) компо-

ненту вектора.

Слева записана сумма – раскроем ее: δ_i^kxⁱ=δ₁^kx¹ +δ₂^kx² +δ₃^kx³ = x^k

Для выполнения равенства нужно, чтобы равнялась единице только та компонента δ_i^k, для которого i = k . А остальные должны быть нулевыми. Значит, единичный тензор выглядит точно как (1.7)

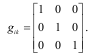
Перейдем к другой системе координат, компоненты вектора изменятся. И единичного

тензора тоже… Но то, что мы разъяснили относительно (1.8), остается, тем не менее, в силе!

Получается, что тензор δ_i^k обладает редким свойством: его компоненты одинаковы в любой системе координат, не изменяются.

Символ Кронекера (или дельта Кронекера) — индикатор равенства элементов, формально: функция двух целых переменных, которая равна 1, если они равны, и 0 в противном случае.

В тензорном исчислении символ Кронекера обычно трактуется как тензор. В частности, могут использоваться различные написания для подчеркивания его принадлежности к определённому типу тензоров; соответственно дважды ковариантным, один раз ковариантным и один контравариантным и дважды контравариантным. При этом важно отметить, что обычная практика обозначать той же буквой тензор после поднятия или опускания индекса не распространяется на дельту Кронекера! Иначе говоря, в общем случае - не представляют один и тот же тензор (за исключением представления в ортонормированных базисах, что, собственно говоря, является признаком, выделяющим ортонормированные базисы из всех)

Основное значение δ-символа Кронекера-это переобозначить буквенное обозначение свободного индекса

Свойства:

дельта-символ симметричен относительно перестановки индексов: δ_ij = δ_ji . (4)

Другое важное свойство дельта-символа δij заключается в том, что он снимает суммирование в выражениях вида

В частности,

В этих обозначениях формула принимает вид