3. Взаимный базис. Способы построения взаимного базиса

Продолжая обсуждение контровариантных и ковариантных компонент вектора уместно поставить вопрос «А какие из них «лучше»?». Сторонники контровариантных компонент, основываясь на выражении a=Σaⁱe_i (1.1), будут утверждать, что при сложении они подчиняются столь «привычному» для нас правилу «параллелограмма». Зато, ковариантные компоненты легко вычислить, в соответствии с a_i=ae_i (1.2), умножить скалярно вектор на соответствующий базисный вектор.

Попытаемся разобраться. Возьмем вектор и разложим его по базисным векторам 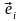, после чего воспользуемся соотношением (1.7) и свойством симметрии фундаментальной матрицы g:

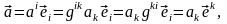(1.8)

В выражении (1.8) введено очевидное обозначение

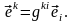(1.9)

Определение 1. Базис образованный вектора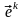ми , построенными из базисных векторов по правилу (1.9), называется взаимным (обратным) к базису образованному векторами

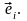
Взаимным базисам можно дать и другое определение. Вычисляя скалярное произведение базисных векторов и прямого и обратного базисов, с учетом (1.9) и (1.5), получаем

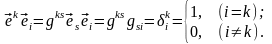(1.10)

Полученный результат известен как условие ортогональности. Он показывает, что, например, первый орт базиса будет ортогонален всем базисным векторам взаимного базиса с номерами

Определение 2. Базисы, орты и которых удовлетворяют соотношению ортогональности (1.10), называются взаимными (обратными) базисами.

Определив необходимые для дальнейшего понятия, перейдем к выяснению сути вопроса. Сравнивая выражение (1.8) с выражением (1.1), можно сделать вывод, что в системе координат определяемой взаимным базисом складывать по правилу «параллелограмма» следует ковариантные компоненты вектора.

Посмотрим, как определяться контровариантные компоненты вектора во взаимном базисе. Для этого умножим скалярно вектор на базисный вектор 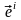взаимного базиса. Учитывая (1.1) и (1.10), будем иметь

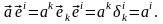(1.11)

Сравнив (1.11) и (1.2) убеждаемся, что во взаимном базисе контровариантные компоненты могут быть рассчитаны по «правилу скалярного произведения».

Таким образом мы, на основании сопоставлений соотношений (1.1) с (1.8) и (1.2) с (1.11) можем сделать вывод, что при переходе от прямого к взаимному базису контровариантные и ковариантные компоненты меняются ролями. Следовательно, вопрос «Каким из них отдать предпочтение?» лишен смысла.

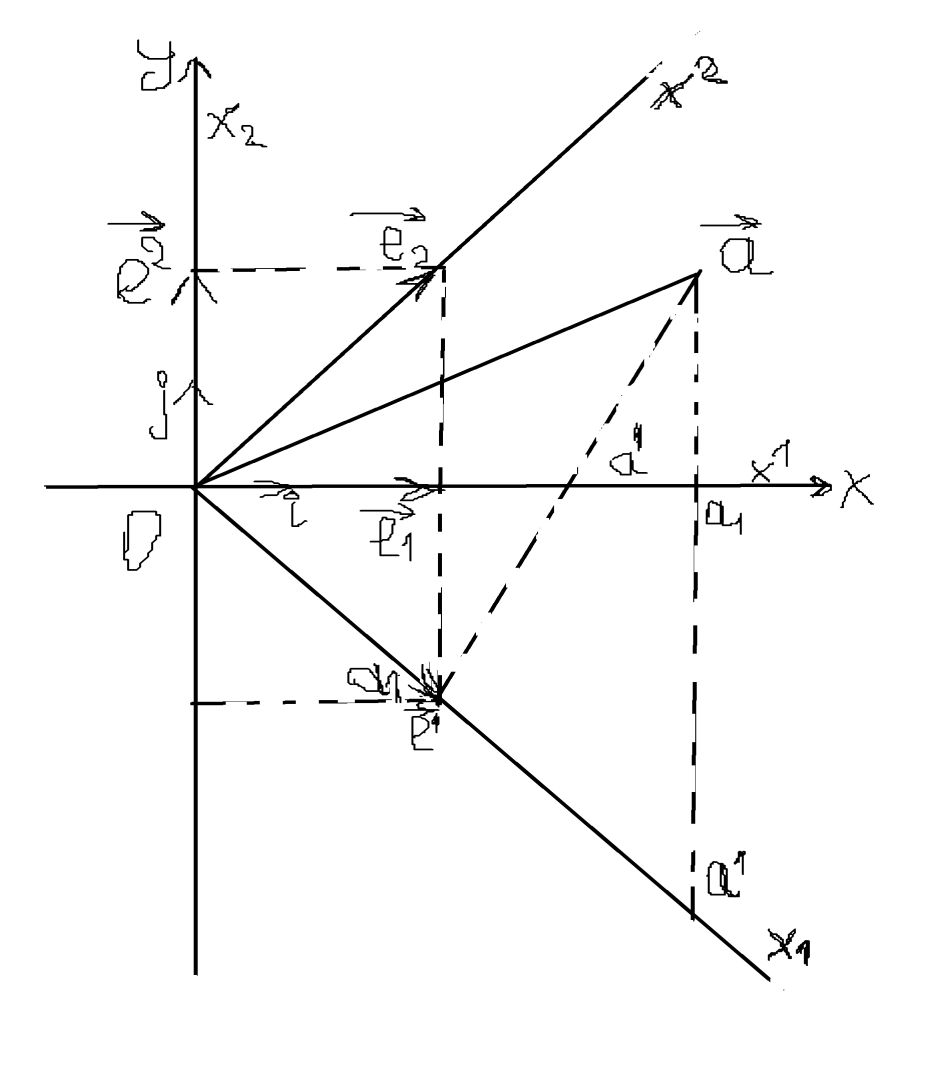
Приведем пример построения взаимного базиса

Пусть e₁={1;0} и e₂={1;1}

Тогда можно построить график:

[g_ij]=[ ]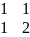

|g|=1 [g^ij]=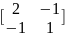

e₁=g¹¹e₁=g¹²e₂=2e₁-e₂={-1;1}

e₂=…={0;1}.

Мы доказали, что при переходе от прямого к взаимному базису контравариантные и ковариантные компоненты меняются ролями.

4. Законы преобразования ковариантных и контравариантных компонент вектора. Свойства законов преобразования.

Переход к «новой»(штрихованной) системы координат К', полученной из «старой»(нештрихованной) системы координат К с помощью ОПСК, запишем в виде

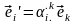(2.1)

Здесь 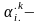элементы матрицы , описывающей ОПСК переводящие систему координат К в систему координат К'.

Обратный переход от системы К' к системе К запишем в виде

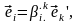(2.2)

где 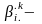элементы матрицы 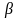обратного преобразования.

Очевидно, что матрица является обратной для матрицы , то есть

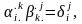(2.3)

где 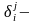символ Кронекера.

Получим законы преобразования компонент вектора при прямом переходе от системы координат К к системе координат K’ и обратном переходе от системы координат К' к системе К, положив в основу рассуждений условие инвариантности 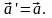Воспользовавшись a=Σaⁱe_i (1.1) ,(2.2) и сформулированным выше требованием, имеем

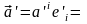
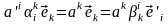
Отсюда, учитывая линейную независимость базисных векторов 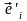, получаем

(2.4)

Аналогично, но используя (2.1), ,

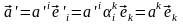находим, что 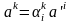. (2.5)

Выражения (2.4) и (2.5) определяют законы преобразования контровариантных компонент вектора при прямом К К' и обратном К' К преобразованиях системы координат.

Получим законы преобразования ковариантных компонент вектора при аналогичных преобразованиях системы координат. Согласно a_i=ae_i (1.2), (2.1) и требования инвариантности можем записать .

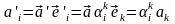Следовательно, при прямом ортогональном преобразовании К К'

(2.6)

Свойства законов преобразования:

1. Однородность (означает, что нет такой точки в пространстве, относительно которой существует некоторая «выделенная» симметрия, все точки равноправны).

2. Линейность (свойство систем или процессов, заключающееся в наличии линейной зависимости одних параметров от других).