22.Политропный процесс. Уравнение политропы, показатель политропы, график политропы.

Политропный процесс - процесс, при котором теплоемкость системы остается постоянной . При таком процессе происходит частичный теплообмен системы с окружающей средой.

Это самый общий процесс, т.к. полностью исключить теплообмен системы с окружающей средой практически невозможно.

I начало ТД для политропного процесса: количество теплоты, передаваемое системе, идет на изменение ее внутренней энергии и совершение системой работы. В дифференциальной форме для одного моля с учетом теплоемкости:

Получим из I начала ТД и уравнения состояния идеального газа уравнение политропного процесса (уравнение политропы)

Продифференцируем уравнение состояния для одного моля идеального газа .

 , подставим в I начало ТД

, перегруппируем подобные слагаемые,

учтем соотношение Майера

разделим на

, введем обозначение отношения , оно называется - показатель политропы.

Разделим переменные и решим дифференциальное уравнение, взяв интеграл:

   отсюда

  .

Уравнение политропы .

Учитывая уравнение состояния, для уравнения политропы, аналогично уравнению адиабаты, есть и другие способы записи:

, .

График политропы на диаграмме состояний в - координатах представляет собой гиперболу, занимающую промежуточное положение между изотермой и адиабатой.

Работа, совершаемая в политропном процессе, вычисляется аналогично работе в изобарическом процессе:

.

Е сли , то работа совершается над газом, газ сжимается.

Изменение внутренней энергии в этом процессе  , как и для всех других процессов в идеальном газе.

Для молей вещества .

Числовые значения показателя политропы определяются опытным путем.

Зависимость теплоемкости от для идеального газа показана на графике.

23.I начало термодинамики в политропном процессе.

I начало ТД для политропного процесса: количество теплоты, передаваемое системе, идет на изменение ее внутренней энергии и совершение системой работы. В дифференциальной форме для одного моля с учетом теплоемкости:

24.Изопроцессы как предельные случаи политропного процесса.

Все изопроцессы могут быть рассмотрены, как предельные случаи политропного процесса.

1. адиабатический процесс .

В этом процессе , показатель политропы превращается в показатель адиабаты .

уравнение политропы превращается в уравнение адиабаты. , , .

2. изотермический процесс .

В этом процессе , показатель политропы равен единице .

уравнение политропы превращается в уравнение изотермы.

, , .

3. изобарический процесс .

В этом процессе , показатель политропы равен нулю .

, уравнение политропы превращается в уравнение изобары.

, , , .

4. изохорический процесс .

В этом процессе , показатель политропы равен бесконечности .

, уравнение политропы превращается в уравнение изохоры.

, , .

25.Обратимые и циклические процессы.

В некоторой изолированной системе тело переходит из состояния 1 в состояние 2, а затем возвращается в состояние 1.

П роцесс называется обратимым, если возможно осуществить обратный переход через те же промежуточные состояния, так, чтобы не осталось никаких изменений в окружающей среде.

Если такой процесс осуществить нельзя, если по окончании процесса в окружающих телах или в самом теле остались какие-либо изменения, то процесс является необратимым.

Любой процесс, сопровождаемый трением, необратим, ибо часть работы при трении всегда превращается в тепло. Трущиеся поверхности нагреваются, и теплота распространяется, рассеивается в окружающих телах. Рассеянная теплота ни при каких процессах не может без затрат энергии, без совершения работы другим телом собраться к трущимся поверхностям и вновь превратится в работу.

Любой реальный механический процесс сопровождается трением и поэтому является необратимым.

Все процессы, сопровождающиеся теплопередачей от нагретого тела к менее нагретому телу, являются необратимыми. Т.к. обратный переход теплоты от холодного тела к нагретому телу, который может быть осуществлен в холодильной машине, не идет сам собой. Для осуществления такого процесса требуется затрата работы еще какого-либо тела, что приводит к изменению в этом теле, и следовательно условие обратимости не выполняются.

Необратимым является процесс расширения газа, даже идеального в пустоту. При таком расширении газ не совершает работы, а чтобы собрать вновь вместе газовые молекулы, сжать газ, привести в начальное состояние, требуется затратить работу, что приведет к изменениям в других телах.

Т.о. все реальные процессы являются необратимыми, хотя степень необратимости может быть разная.

Обратимыми являются квазистатические равновесные процессы. Абстрактные, идеализированные процессы.

Процесс, при котором тело проходить через ряд различных состояний, а в результате возвращается в исходное, начальное состояние называется круговым или цеклическим. Круговой процесс является обратимым, если все его части обратимы. Если какая-либо часть процесса является необратимой, то процесс необратим.

Н а диаграмме состояний в -координатах круговой процесс представляет собой замкнутую кривую. В процессе, происходящем по часовой стрелке 1а2в1, теплота превращается в механическую работу. В процессе идущем против часовой стрелки 1в2а1 механическая энергия превращается в теплоту, точки 1 и 2 соответствуют начальному и промежуточному значениям давлений и объемов , .

Система, которая совершает круговой процесс, обмениваясь энергией (теплотой) с внешней средой называют рабочим телом.

Система после получения в начальном состоянии 1 определенное количество теплоты от нагревателя совершает положительную работу и переходит в промежуточное состояние 2. Затем после теплового контакта с холодильником, она отдает ему часть количества теплоты и за счет совершения работы над системой , возвращается в исходное состояние 1.

Т.к. после окончания кругового процесса рабочее тело возвращается в исходное состояние, его внутренняя энергия не изменяется. Поэтому рабочее тело может совершать работу только за счет внешних источников, подводящих к нему теплоту.

Т.о. изолированная система в целом не может совершить круговой процесс, т.к. требуется участие внешних сил, внешних источников тепла.

Р абота, совершаемая за круговой процесс (цикл) рабочим телом, равна площади внутри замкнутой кривой кругового процесса. , , .

В принципе существует бесчисленное множество возможных циклов, поскольку каждой замкнутой кривой, на диаграмме в - координатах соответствует цикл. Можно представить различные круговые процессы, используя уже изученные процессы и их комбинации. Например, процессы, изображенные в - координатах:

а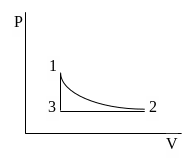 ) круговой процесс, в котором рабочее тело совершает два изобарических (1-2, 4-3) и два изохорических процесса (2-3, 4-1);

б ) круговой процесс, в котором рабочее тело совершает изотермический (1-2), затем изобарический (2-3) и изохорический (3-1) процессы;

в) круговой процесс, в котором рабочее тело совершает адиабатический (1-2), затем изобарический (2-3) и изохорический (3-1) процессы;

г) круговой процесс, в котором рабочее тело совершает два изотермических (1-2, 3-4) и два адиабатических (2-3, 4-1) процесса.