2.3 Построение модели выручки предприятия

Построим аддитивную модель на основе данных квартальной отчетности, чтобы оценить динамику выручки ООО «Элвина+» за 3 года и составить прогноз.

Таблица 15

Расчетные данные для построения модели

	I квартал	II квартал	III квартал	IV квартал
2009 год	980055	1084625	1365238	1290732
2010 год	980172	1104430	1424139	1301465
2011 год	1209020	1384029	1590111	1401216

Коэффициент автокорреляции измеряет зависимость между соседними уровнями ряда t. Определим коэффициент автокорреляции первого порядка (Приложение, таблицы 5-12)

Нанесем значения на график.

Рис. Выручка предприятия

Рис 5. График выручки предприятия

_{Коэффициент автокорреляции 1 порядка:}

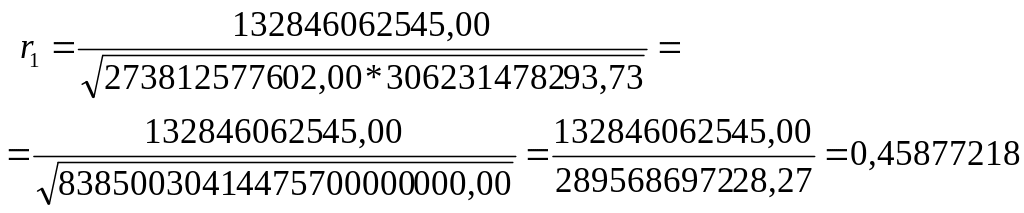
_{Это значение свидетельствует о средней зависимости текущих уровней ряда от непосредственно предшествующих. Но структура ряда такова, что не каждый уровень сильно зависит от предыдущего. Рассчитаем коэффициенты автокорреляции больших порядков.}

_{Коэффициент автокорреляции второго порядка:}

_{Коэффициент автокорреляции третьего порядка:}

_{Коэффициент автокорреляции четвертого порядка:}

_{Коэффициент автокорреляции пятого порядка:}

_{Коэффициент автокорреляции шестого порядка:}

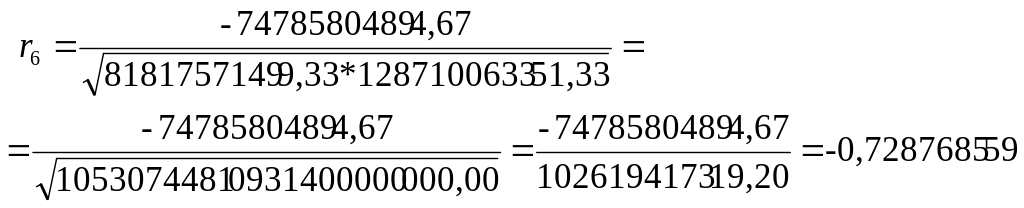
_{Коэффициент автокорреляции седьмого порядка:}

_{Коэффициент автокорреляции восьмого порядка:}

_{Кореллограмма временного ряда:}

Лаг	К-т автокорреляции	Лаг	К-т автокорреляции
1	0,4588	5	0,2789
2	0,3968	6	0,7288
3	0,3153	7	0,5069
4	0,8408	8	0,8995

Расчет коэффициента автокорреляции до 8 порядка подтвердил «пилообразную» структуру графика, показав периодичность в 4 квартала.

Перейдем непосредственно к построению аддитивной модели. Проведем выравнивание исходных уровней ряда методом скользящей средней.

1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы;

2) разделив полученные суммы на 4, найдем скользящие средние. Таким образом, выровненные значения уже не содержат сезонной компоненты;

3) приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.

Затем найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними. Используем эти оценки для расчета значений сезонной компоненты S. [24, c. 220]

Таблица 16

Расчет оценок сезонной компоненты

№ квартала	yt	Итого за год	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	980055	-
2	1084625	4720650	1180162,5
3	1365238	4720767	1180191,75	1180177,125	185 061
4	1290732	4740572	1185143	1182667,375	108064,625
5	980172	4799527	1199881,75	1192512,375	-212340,375
6	1104430	4810260	1202565	1201223,375	-96793,375
7	1424193	5039108	1259777	1231171	193022
8	1301465	5318707	1329676,75	1294726,875	6738,125
9	1209020	5484625	1371156,25	1350416,5	-141396,5
10	1384029	5584376	1396094	1383625,125	403,875
11	1590111
12	1401216
Сумма				10016519,75	0

В моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Таблица 17

Расчет значений сезонной компоненты в аддитивной модели

Показатель	Год	Номер квартала, i
		I	II	III	IV
	1			185061	108064,625
	2	-212340,375	-96 793,38	193022	6738,125
	3	-141396,5	403,88
Итого за квартал	*	-353736,875	-96 389,50	378083	114802,75
Средняя оценка сезонной компоненты Si	*	-176868,4375	-48194,75	189041,5	57401,375
Скорректированная сезонная компонента Si	*	-182213,359375	-53539,67188	183696,57812	52056,45312

Для данной модели имеем:

-176868,4375-48194,75+189041,5+57401,375 = 21379,6875

Определим корректирующий коэффициент

К= 21379,6875/4 = 5344,921875

Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и коэффициентом К и внесем их в последнюю строку таблицы:

Si=S_i – K; (7)

Проверим условие равенства нулю суммы значений сезонной компоненты:

-182213,359375 -53539,671875 +183696,578125+ 52056,453125=0

Таким образом, получены следующие значения сезонной компоненты:

I квартал = -182213,359375

II квартал = -53539,671875

III квартал = 183696,578125

IV квартал = 52056,453125

Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим Т+Е=Y-S. Эти значения содержат лишь тенденцию и случайную компоненту.

Таблица 18

Расчет данных для нахождения компоненты Т по модели

t	yt	Si	T+E=yt-Si		(T+E)*t
1	980055	-182213,3594	1 162 268	1	1162268,359
2	1084625	-53539,6719	1 138 165	4	2276329,344
3	1365238	183696,5781	1 181 541	9	3544624,266
4	1290732	52056,4351	1 238 676	16	4954702,26
5	980172	-182213,3594	1 162 385	25	5811926,797
6	1104430	-53539,6719	1 157 970	36	6947818,031
7	1424193	183696,5781	1 240 496	49	8683474,953
8	1301465	52056,4351	1 249 409	64	9995268,519
9	1209020	-182213,3594	1 391 233	81	12521100,23
10	1384029	-53539,6719	1 437 569	100	14375686,72
11	1590111	183696,5781	1 406 414	121	15470558,64
12	1401216	52056,4351	1 349 160	144	16189914,78
78	15115286		15 115 286	650	101933672,9

Произведем расчет выровненных значений Т и ошибок Е в аддитивной модели (Приложение, таблица 13).

₍₈₎

a=(15115286 – 78b)/12=1259607,1- 6,5b;

78 (1259607,1 - 6,5b) + 650b = 98249353 - 507b + 650b=101933672,9;

143b=3684319,9;

b=25764,47

a=1259607,1-167469,05=1092138,302

Таким образом, имеем линейный тренд:

ˆ

T=a+bt = 1092138,302 – 25764,47t

Подставив в данное уравнение значения t, мы сможем найти уровни Т для каждого момента времени.

Рис 6. График уравнения тренда

В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле: E = Y – (T+S)

Это абсолютная ошибка. Численные значения приведены в предпоследнем столбце таблицы 13 Приложения.

Найдем коэффициент детерминации для линии тренда.

₍₉₎

Соответственно 73% тенденции объяснено временем.

В линейном тренде оценивается значимость отдельных его параметров.

1. _{Проверим значимость параметра b:}

_{Следовательно, параметр b статистически значим.}

_{2) Проверим значимость параметра a:}

_{Следовательно, параметр a статистически значим, и уравнение имеет вид:}

ˆ

T = 1092138,302+ 25764,47t

_{Найдем среднюю ошибку аппроксимации, которая показывает соответствие расчетных данных фактическим.}

Таким образом, модель имеет вид:

По этой модели можно вычислить, какой при прочих равных условиях будет выручка предприятия в ближайшее время. Рассчитаем ее значение на 4 квартала 2012 года. По кварталам t примет значения 13, 14, 15 и 16 соответственно:

Расчет показывают, что выручка сохранит тенденцию дальнейшего роста, что положительно характеризует действия менеджмента предприятия, предпринятые за отчетный год. Сопоставим сумму рассчитанной по модели выручки с себестоимостью реализованной за отчетный год продукции.

По данным отчета о прибылях и убытках, себестоимость составляла 6 578 058 р. С учетом снижения себестоимости за прошлый период на 9,69%, получим при прочих равных условиях значение 5 940 644,2 р. Суммарная годовая выручка равнялась 5 584 376 р, выручка же, рассчитанная по модели составляет 5 862 892,5 р. По текущему расчету, для покрытия даже сниженной себестоимости необходимо увеличить годовой доход на 77 751 р.

Составим прогноз еще на 4 квартала, чтобы узнать, сможет ли предприятие поднять выручку до точки безубыточности при прочих равных условиях в 2013 году.

В сумме по всем кварталам получаем значение 6275123,99 р., что превышает сниженную себестоимость продаж на 334 479,79. Таким образом, не прибегая к новым мерам, при прочих равных условиях, «Элвина+» начнет получать прибыль от продаж только в 2013 году.