27.Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с очередями.
Системы массового обслуживания - это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.
В СМО с очередями заявка, поступившая в систему в момент времени, когда свободен хотя бы один канал, обслуживается немедленно. Если же все каналы заняты, то поступившая заявка становится в очередь и ожидает обслуживания.
Рассмотрим несколько видов СМО с очередями:
1) Одноканальная СМО с неограниченной очередью.
Интенсивность поступления заявок равна λ. Интенсивность обслуживания заявок равна µ.
Уравнения Колмогорова для вероятностей состояний:
Стационарный режим функционирования данной СМО существует при t→ для любого n = 0, 1, 2, ... и когда λ<µ.
Решение системы имеет вид:
,
при n = 0, 1, 2, ..., где
.
Среднее число находящихся в системе заявок на обслуживание:
Средняя продолжительность пребывания заявки в системе:
Среднее число заявок в очереди на обслуживании:
Средняя продолжительность пребывания заявки в очереди:
.
2) Одноканальная СМО с ограниченной очередью.
Здесь независимо от того, сколько заявок поступает на вход обслуживающей системы, данная система не может вместить более N заявок, т.е. заявки, не попавшие в ожидание, вынуждены обслуживаться в другом месте.
Состояния СМО имеют следующую интерпретацию:
S0 – «канал свободен»;
S1 – «канал занят» (очереди нет);
S2 – «канал занят» (одна заявка стоит в очереди);
…
Sn – «канал занят» (n-1 заявок стоит в очереди);
SN – «канал занят» (N-1 заявок стоит в очереди).
Стационарное решение системы имеет вид:
,
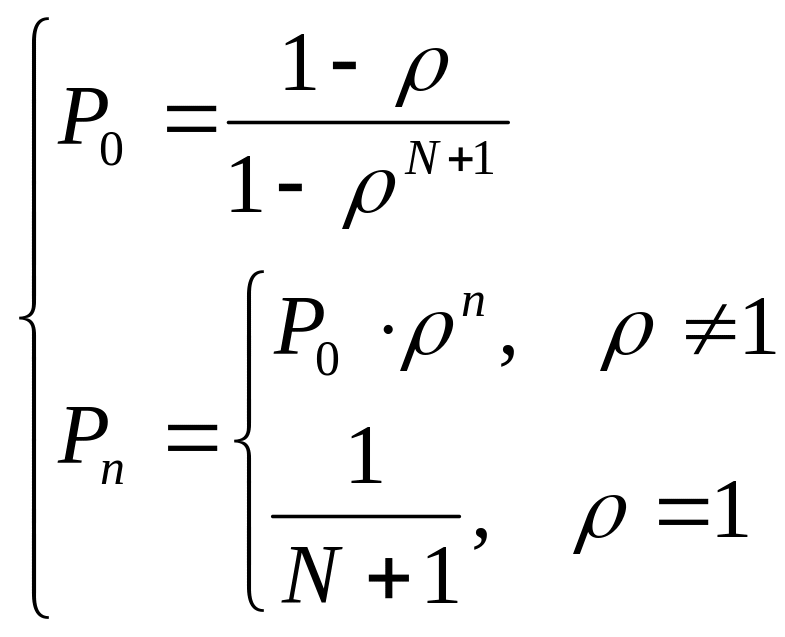при n = 0, 1, 2, ..., N.
Вероятность отказа в обслуживании заявки:
Относительная пропускная способность:
Абсолютная пропускная способность:
Среднее число находящихся в системе заявок на обслуживание:
Средняя продолжительность пребывания заявки в системе:
Средняя продолжительность пребывания заявки в очереди:
Среднее число заявок в очереди на обслуживании:
.
3) Многоканальная СМО с неограниченной очередью.
Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока λ, при этом параллельно может обслуживаться не более S заявок. Средняя продолжительность обслуживания одной заявки равняется 1/µ.
Уравнения Колмогорова для вероятностей состояний:
Стационарный режим функционирования данной СМО существует при (ρ/S)<1.
Решение системы имеет вид:
,
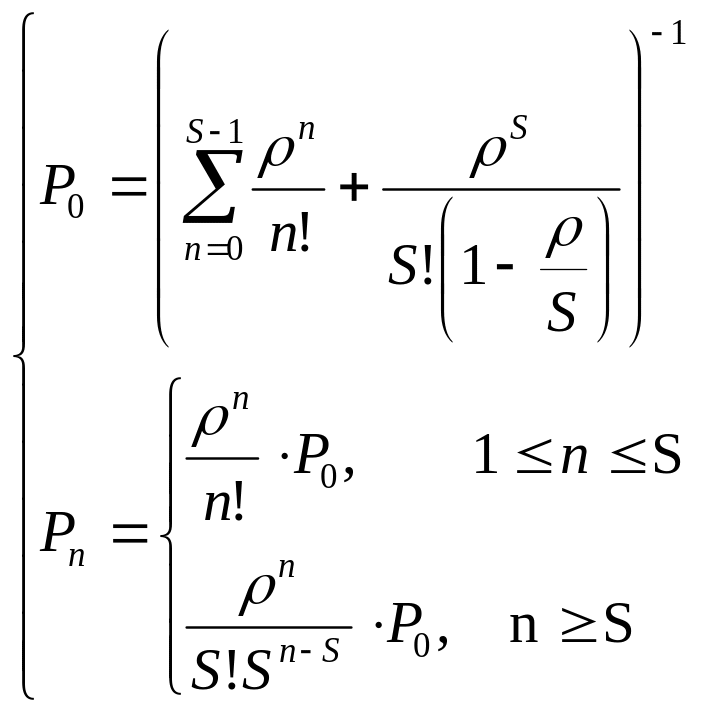при n = 0, 1, 2, ...,.
Среднее число заявок в очереди на обслуживании:
Средняя продолжительность пребывания заявки в очереди:
.
Среднее число находящихся в системе заявок на обслуживание:
Средняя продолжительность пребывания заявки в системе:
28.Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с отказами.
Смотри вопрос №26.