
- •1.Дайте определение и определите сущность системного подхода к моделированию систем
- •2.Дайте определение системы и перечислите основные характеристики системы.
- •3.Укажите цель моделирования системы на эвм
- •4.Дайте описание основных задач моделирования систем
- •5.Приведите приемы формализации задач моделирования
- •6.Укажите основные типы моделей систем, дайте определение математического моделирования системы
- •7. Опишите признаки классификации типовых математических схем, приведите схему классификации
- •8. Определение онтологии, основные ее компоненты
- •9. Приведите описание методики онтологического анализа.
- •10. Дайте определение математической схемы, укажите, что понимается под законом функционирования системы
- •11. Опишите, что понимается под алгоритмом функционирования систем.
- •12. Дайте определение статической и динамической моделей объекта
- •12.Дайте определение статической и динамической моделей объекта
- •13.Перечислите, какие типовые математические схемы используются при моделировании сложных систем и их элементов
- •14.Каковы условия и особенности использования при разработке моделей систем непрерывно-детерминированных моделей (d-схем)
- •15.Каковы условия и особенности использования при разработке моделей систем дискретно-детерминированных моделей (f-схем)
- •16.Дайте определение конечного автомата, укажите основные соотношения математической схемы конечного автомата
- •17. Приведите уравнения работы автомата Мили (f-автомата первого рода)
- •18. Приведите уравнения работы автомата Мура (f-автомата второго рода)
- •19. Дайте определение вероятностного конечного автомата (p-схемы), укажите основные соотношения математической схемы вероятностного автомата
- •20. Дайте определение типовых математических схем массового обслуживания (q-схем), укажите основные соотношения математической схемы процесса обслуживания
- •21. Дайте определение сетевой модели (n-схемы), укажите основные соотношения сети Петри
- •22. Дайте характеристику метода статистического моделирования систем на эвм
- •23.Опишите способы генерации последовательности случайных чисел, используемые при моделировании систем на эвм
- •24.Опишите, что представляют собой конгруэнтные процедуры генерации последовательностей
- •25.Укажите, какие функции используются для генерации случайных чисел с различными законами распределения в системе matlab
- •26.Дайте определение и приведите основные соотношения для моделирования систем массового обслуживания с отказами.
- •27.Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с очередями.
- •28.Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с отказами.
- •29.Дайте определение и приведите основные соотношения для моделирования замкнутых систем массового обслуживания.
- •30.Приведите пример моделирования системы массового обслуживания на эвм.
- •31. Проанализируйте процесс построения модели системы
- •32.Дайте определение и опишите сущность имитационного моделирования систем
- •33.Перечислите известные инструментальные средства моделирования систем
- •34. Опишите функциональные возможности пакета прикладных программ matlab как средства моделирования систем
- •35.Опишите основные этапы процесса формализации и алгоритмизации процесса функционирования систем
- •37. Основные принципы принятия решений, сформулируйте проблему принятия решений
- •1.Разработка и машинная реализация моделей систем
- •2. Построение концептуальных моделей систем и их формализация
- •3. Алгоритмизация моделей систем и их машинная реализация
- •4. Получение и интерпретация результатов моделирования систем
- •40.Дайте определение и сформулируйте поставку задач математического программирования
- •41.Приведите классификацию моделей математического программирования
- •42. Рассмотрите содержательные постановки задач, приводящие к моделям линейного программирования
- •43. Дайте общую математическую формулировку задачи линейного программирования
- •44. Рассмотрите пример графического решения задачи линейного программирования
- •45.Опишите процесс решения задачи линейного программирования симплекс-методом
- •46.Рассмотрите пример решения задачи линейного программирования симплекс-методом
- •47.Опишите процесс решения задач линейного программирования с использованием программного обеспечения matlab
- •48.Дайте общую математическую формулировку задач дискретного программирования
- •49.Приведите содержательные постановки задач, приводящие к моделям дискретного программирования.
- •50.Дайте общую математическую формулировку задач нелинейного программирования
- •51.Поясните понятия: задача многокритериальной оптимизации, множество допустимых решений, оптимальное решение. Дайте общую математическую формулировку задач многокритериальной оптимизации
21. Дайте определение сетевой модели (n-схемы), укажите основные соотношения сети Петри
В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов.
Теория сетей Петри развивается в нескольких направлениях: разработка математических основ, структурная теория сетей, различные приложения (параллельное программирование, дискретные динамические системы и т. д.).
Сеть Петри состоит из 4 компонентов, которые и определяют ее структуру:
- множество позиций Р,
- множество переходов Т,
- входная функция I,
- выходная функция О.
Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход tj в множество позиций I(tj), называемых входными позициями перехода. Выходная функция О отображает переход tj в множество позиций О(tj), называемых выходными позициями перехода. Т.е.
( I : T -> P) (O : T -> P).
Определение 1. Сеть Петри С является четверкой С = (P,T,I,O) где
Р={p1,p2,...,pn} конечное множество позиций, n>=0.
T={t1,t2,...,tm} конечное множество переходов, m>=0.
Множества позиций и переходов не пересекаются.
I : T -> P является входной функцией - отображением из переходов в комплекты позиций.
O : T -> P выходная функция - отображение из переходов в комплекты позиций.
Мощность множества Р есть число n, а мощность множества Т есть число m. Произвольный элемент Р обозначается символом pi, i=1...n; а произвольный элемент Т - символом tj, j=1...m.
![]()
рис. 1
Позиция pi является входной позицией перехода tj, в том случае, если pi I(tj);
pi является выходной позицией перехода, если pi O(tj).
![]()
рис. 2
Входы и выходы переходов представляют комплекты позиций. Кратность входной позиции для перехода tj есть число появлений позиции во входном комплекте перехода #(pi,I(tj)). Аналогично, кратность выходной позиции pi для перехода tj есть число появлений позиции в выходном комплекте перехода #(pi,O(tj)).
Определим, что переход tj является входом позиции pi, если pi есть выход tj (рис. 2). Переход tj есть выход позиции pi, если pi есть вход tj (рис. 1).
Графически N-схема изображается в виде двудольного ориентированного
мультиграфа, представляющего собой совокупность позиций и переходов
(рис. 2.8). Как видно из этого рисунка, граф N-схемы имеет два типа узлов:
позиции и переходы, изображаемые 0 и 1 соответственно.
Ориентировочные
дуги соединяют позиции и переходы,
причем каждая дуга направлена от элемента
одного множества (позиции или перехода)
к элементу другого множества (переходу
или позиции). Граф N-схемы является
мультиграфом, так как он допускает
существование кратных дуг от одной
вершины к другой.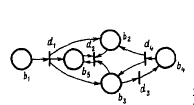
Рис. 28. Графическое изображение
