43 Вопрос наименьшее общее кратное.Наибольший общий делитель.Нахождение нод и нок данных чисел. ( в учебнике страница 356)

Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.^[1] Пример: для чисел 70 и 105 наибольший общий делитель равен 35.

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не ноль.

Возможные обозначения наибольшего общего делителя чисел m и n:

• НОД(m, n)

• (m, n)

• gcd(m, n) (от англ. Greatest Common Divisor)

Понятие наибольшего общего делителя естественным образом обобщается на наборы из более чем двух целых чисел.

Связанные определения Наименьшее общее кратное

Основная статья: Наименьшее общее кратное

Наименьшее общее кратное (НОК) двух целых чисел m и n — это наименьшее натуральное число, которое делится на m и n. Обозначается НОК(m,n) или , а в английской литературе lcm(m,n).

НОК для ненулевых чисел m, n всегда существует и связан с НОД следующим соотношением:

Это частный случай более общей теоремы: если — ненулевые числа, D — какое-либо их общее кратное, то имеет место формула:

Взаимно простые числа

Основная статья: Взаимно простые числа

Числа m и n называются взаимно-простыми, если у них нет общих делителей, кроме единицы. Для таких чисел НОД(m,n) = 1. Обратно, если НОД(m,n) = 1, то числа взаимно просты.

Аналогично, целые числа , где , называются взаимно простыми, если их наибольший общий делитель равен единице.

Следует различать понятия взаимной простоты, когда НОД набора чисел равен 1, и попарной взаимной простоты, когда НОД равен 1 для каждой пары чисел из набора. Из попарной простоты вытекает взаимная простота, но не наоборот. Например, НОД(6,10,15) = 1, но любые пары из этого набора не взаимно просты.

Способы вычисления

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм.

Кроме того, значение НОД(m,n) можно легко вычислить, если известно каноническое разложение чисел m, n на простые множители:

где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД(m,n) и НОК(m,n) выражаются формулами:

Если чисел более двух: , их НОД находится по следующему алгоритму:

………

— это и есть искомый НОД.

Свойства

• Основное свойство: наибольший общий делитель m и n делится на любой общий делитель этих чисел. Пример: для чисел 12 и 18 наибольший общий делитель равен 6; он делится на все общие делители этих чисел: 1, 2, 3, 6.

  • Следствие 1: множество общих делителей m, n совпадает с множеством делителей НОД(m, n).

  • Следствие 2: множество общих кратных m, n совпадает с множеством кратных НОК(m, n).

• Если m делится на n, то НОД(m, n) = n. В частности, НОД(n, n) = n.

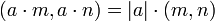•  — общий множитель можно выносить за знак НОД.

• Если 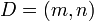, то после деления на D числа становятся взаимно простыми, то есть, . Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.

• Мультипликативность: если взаимно просты, то:

• Наибольший общий делитель чисел m и n может быть определён как наименьший положительный элемент множества всех их линейных комбинаций:

и поэтому (m,n) представим в виде линейной комбинации чисел m и n:

.

Это соотношение называется соотношением Безу, а коэффициенты u и v — коэффициентами Безу. Коэффициенты Безу эффективно вычисляются расширенным алгоритмом Евклида. Это утверждение обобщается на наборы натуральных чисел — его смысл в том, что подгруппа группы , порождённая набором , — циклическая и порождается одним элементом: НОД .