Логика предикатов

Понятие предиката. Значение формулы логики предикатов. Общезначимость и выполнимость формул. Проблема разрешимости. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений. Доказательство теорем методом от противного

Понятие предиката

В алгебре логики высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности.

Ни структура высказываний, ни, тем более, их содержание не затрагиваются. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.

Например, в рассуждении “Всякий ромб – параллелограм; АВСD – ромб; следовательно, АВСD - параллелограм ” посылки и заключение являются элементарными высказываниями логики высказываний и с точки зрения этой логики рассматриваются как целые, неделимые, без учета их внутренней структуры. Следовательно, алгебра логики, будучи важной частью логики, оказывается недостаточной в анализе многих рассуждений.

В связи с этим возникает необходимость в расширении логики высказываний, в построении такой логической системы, средствами которой можно было бы исследовать структуру тех высказываний, которые в рамках логики высказываний рассматриваются как элементарные.

Такой логической системой является логика предикатов, содержащая всю логику высказываний в качестве своей части.

Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально – подлежащее, хотя оно может играть и роль дополнения) и предикат (буквально – сказуемое, хотя оно может играть и роль определения).

Субъект – это то, о чем что-то утверждается в высказывании;

предикат – это то, что утверждается о субъекте.

Например, в высказывании “7 - простое число”, “7” – субъект, “простое число” – предикат. Это высказывание утверждает, что “7” обладает свойством “быть простым числом”.

Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму “х – простое число”. При одних значения х (например, х=13, х=17) эта форма дает истинные высказывания, а при других значениях х (например, х=10, х=18) эта форма дает ложные высказывания.

Ясно, что эта высказывательная форма определяет функцию одной переменной х, определенной на множестве N, и принимающую значения из множества {1;0}. Здесь предикат становится функцией субъекта и выражает свойство субъекта.

Областью значений предиката является двухэлементное множество B={true, false}. При этом сами переменные x₁,...,x _n называются предметными переменными, т.е. их значения не являются логическими ( не принадлежат множеству B).

Понятие ``предикат'' обобщает понятие ``высказывание''. Неформально говоря, предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами.

Так как значениями предикатов являются true или false, то сами предикаты можно рассматривать как логические переменные. Из них можно составлять сложные логические выражения, образованные из простых предикатов с помощью знаков логических операций. После подстановки в такое составное выражение конкретных значений предметных переменных получается сложное высказывание, значение которого определяется истинностью или ложностью входящих в него простых высказываний и логическими операциями.

Определение 1. Логика предикатов, раздел математической логики, изучающий логические законы, общие для любой области объектов исследования (содержащей хоть один объект) с заданными на этих объектах предикатами (т. е. свойствами и отношениями).

В результате формализации логика предикатов принимает вид различных исчислений. Простейшими логическими исчислениями являются исчисления высказываний. В более сложных исчислениях предикатов описываются логические законы, связывающие объекты исследования с отношениями между этими объектами.

В классическом исчислении предикатов употребляются следующие знаки: 1) т. н. предметные переменные — буквы х, у, z,..., которые содержательно рассматриваются как неопределённые имена объектов исследования теории; 2) предикатные переменные — знаковые комплексы вида P^m, Qⁿ, R^l,... (m, n, l — натуральные числа), причём, например, Qⁿ означает произвольное n-местное отношение между объектами; 3) знаки для логических связок: конъюнкции &, дизъюнкции , импликации , отрицания , означающие соответственно «... и...», «... или...», «если..., то...», «неверно, что...»; 4) знаки для кванторов  (квантор всеобщности),  (квантор существования), означающие соответственно «для всех...» и «существует... такое, что...»; 5) запятая, скобки (для уточнения строения формул).

Определение 2 Квантор (от лат. quantum — сколько), логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения.

В обычном языке носителями таких характеристик служат слова типа «все», «каждый», «некоторый», «существует», «имеется», «любой», «всякий», «единственный», «несколько», «бесконечно много», «конечное число», а также все количественные числительные. В формализованных языках, составной частью которых является исчисление предикатов, для выражения всех подобных характеристик оказывается достаточным кванторов двух видов: Квантор всеобщности (оборот «для всех х», обозначается через x, и Квантор существования («для некоторых х», обозначения: x.

С помощью кванторов можно записать четыре основных формы суждений традиционной логики: «все А суть В» записывается в виде x [A (x) B (x)], «ни одно A не есть B» — в виде x [A (x) B (x)], «некоторые А суть B» — в виде x [A (x)B (x)], «некоторые А не суть В» — в виде x [A (x) B (x)] (здесь А (х) означает, что х обладает свойством A).

Часть формулы, на которую распространяется действие каких-либо Квантора, называется областью действия этого Квантора (её можно указать с помощью скобок). Применение Квантора уменьшает число свободных переменных в логическом выражении и превращает (если Квантор не «фиктивный», т. е. относится к переменной, действительно входящей в формулу) трёхместный предикат в двухместный, двухместный — в одноместный, одноместный — в высказывание.

Определение 3. Одноместным предикатом Р(x) называется произвольная функция переменной x, определенная на множестве M и принимающая значение из множества {1; 0}.

Определение 4. Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x).

Множество всех элементов 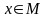, при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множество или иначе: или так: Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности I_P для него есть множество всех простых чисел.

Предикат Q(x) – “sin(x)=0” определен на множестве R, а его множеством истинности является

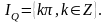
Предикат F(x) – “диагонали параллелограма x взаимно перпендикулярны” определен на множестве всех параллелограмов, а его множеством истинности является множество всех ромбов.

Из приведенных примеров видим, что одноместные предикаты выражают свойства предметов (субъектов).

Определение 5. Предикат Р(х), определенный на множестве М, называется тождественно истинным, если его множество истинности совпадает с областью определения, т. е. I_p=M.

Определение 6. Предикат Р(х), определенный на множестве М, называется тождественно ложным, если его множество истинности является пустым множеством, т. е. I_p=0.

Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами.

Примером бинарного отношения, т. е. отношения между двумя предметами, является отношение “меньше ”. Пусть это отношение введено на множестве Z целых чисел. Оно может быть охарактеризовано высказывательной формой “х<y”, где , то–есть является функцией двух переменных Р(х,y), определенной на множестве упорядоченных пар целых чисел ZхZ=Z² c множеством значений {1;0}.

Определение 7. Двухместным предикатом Р(x,y) называется функция двух переменных x и y, определенная на множестве М=М₁хМ ₂ и принимающая значения из множества {1;0}.

В числе примеров двухместных предикатов можно назвать такие предикаты: Q(x, y) – “x=y” - предикат равенства, определенный на множестве RхR=R²; F(x,y) – “х параллелен y”, “прямая х параллельна прямой y”, определенный на множестве прямых, лежащих на данной плоскости.

Совершенно аналогично вводится понятие трехместного предиката. Приведем пример трехместного предиката (функции трех переменных): S(x,y,z) – “x+y=z”. Подстановка в него х=3 превращает его в двухместный предикат: S(y,z) – “3+y=z”, а подстановка х=3, z=2 – в одноместный предикат S(y) – “3+y=2”.Подстановка же S(2,3,5) превращает его в истинное высказывание, а S(1,7,4)– в ложное.

Аналогично определяется и n-местный предикат (функция n переменных). Пример п- местного предиката:

R(x₁, x₂,…,x_n): a₁ x₁+…+a_nx_n=0,

который, как видим, представляет собой алгебраическое уравнение с n неизвестными.

При n=0 будем иметь нульместный предикат – это логическая (пропозициональная) переменная, принимающая значения из множества {1;0}.

Исторически понятие о предикате явилось следствием логического анализа высказываний естественного языка, т. е. выяснения их логической структуры, выяснения того, какой логикой может быть выражен (формализован) смысл этих высказываний. Идея выделения логической структуры речи, в отличие от грамматической, для нужд логической дедукции принадлежит Аристотелю. В аристотелевской и в последующей «традиционной» логике П. понимался в узком смысле как один из двух терминов суждения, а именно тот, в котором нечто говорится о предмете речи — субъекте. Форма сказывания — предикативная связь — сводилась при этом к атрибутивной связи, т. е. выражала «присущность» предмету некоторого признака. Аристотель выделял 4 типа признаков, способных играть роль предиката.: родовые, видовые, собственные и случайные. Это т. н. предикабилии — типы сказуемых.

Основой для «функциональной» точки зрения на предикат служат в естественных и в искусственных (точных) языках выражения вида повествовательных предложений, содержащие неопределённые термины — неопределённые имена предметов: переменные (параметры) в записи утверждений в математическом языке, например х + 2 = 4; слова «нечто», «некто», «кто-либо» и пр., играющие в естественном языке роль переменных в выражениях типа: «Некто человек», «Кто-то любит кого-то», «Если кто-либо человек, то он смертен» и т.п. Записав эти выражения некоторым единым способом, например заменяя неопределённые термины пробелами, аналогично тому, как это делается в опросных бланках, «—+ 2 = 4», «—человек», «— любит —», «Если — человек, то — смертен», или же принимая запись с помощью переменных в качестве основной, «x + 2 = 4», «x человек», «х любит у», «Если х человек, то х смертен», легко заметить нечто общее между ними. Во-первых, наличие неопределённых терминов делает эти и подобные им выражения, вообще говоря, неопределёнными как в смысле того, что в них утверждается, так и в смысле их истинностного значения; во-вторых, всякое подходящее указание на область значений неопределённых терминов и одновременная квантификация или замена неопределённых терминов их значениями преобразует соответствующие выражения в осмысленные высказывания. В современной логике выражения, имеющие вид повествовательных предложений и содержащие неопределённые термины, получили общее название пропозициональных функций, или, сохраняя традиционный термин, предикатов. Как и числовые функции, предикаты. являются соответствиями. Неопределённые термины играют в них обычную роль аргументов функции, но, в отличие от числовых функций, значениями предикатов. служат высказывания. В общем случае, отвлекаясь от какого-либо определённого языка и сохраняя только функциональную форму записи, предикат от n переменных (от n неопределенных терминов) выражают формулой P (x₁,..., x_n), где n  0. При n = 0 предикат совпадает с высказыванием, при n = 1 предикат будет свойством в узком смысле (1-местным предикатом), при n = 2 — свойством «пары» (2-местным предикатом, или бинарным отношением), при n = 3 — свойством «тройки» (3-местным предикатом, или тернарным отношением) и т.д.

Примеры предикатов:

1. Возьмём высказывания: ``Сократ - человек'', ``Платон - человек''. Оба эти высказывания выражают свойство ``быть человеком''. Таким образом, мы можем рассматривать предикат ``быть человеком'' и говорить, что он выполняется для С0ократа и Платона.

2. Возьмём высказывание: ``расстояние от Иркутска до Москвы 5 тысяч километров''. Вместо него мы можем записать предикат ``расстояние'' (означающий, что первый и второй аргумент этого предиката находятся на расстоянии, равном третьему аргументу) для аргументов ``Иркутск'', ``Москва'' и ``5 тысяч километров''.

3. Высказывание "у каждого человека есть отец" можно записать:

 x y (человек(x) отец(y,x))

3. Выражение "Джон владеет красной машиной" записывается, например, так:

x ( владеет(Джон, x) машина(x) &красный(x))

4. Выражение «все простые числа больше чем x» можно записать

 y(P (y)  Q(x, y)). , где

• P(x) выражает условие ``x является простым числом'',

• Q(x, y) выражает условие ``x меньше чем y''.

5. Выражение "у всех людей общий отец".

y x (человек(x) отец(y,x))

Значение формулы логики предикатов

О логическом значении формулы логики предикатов можно говорить лишь тогда, когда задано множество M, на котором определены входящие в эту формулу предикаты. Логическое значение формулы логики предикатов зависит от значений трех видов переменных: 1) значений входящих в формулу переменных высказываний, 2) значений свободных предметных переменных из множества М, 3) значений предикатных переменных.

При конкретных значениях каждого из трех видов переменных формула логики предикатов становится высказыванием, имеющим истинное или ложное значение.

В качестве примера рассмотрим формулу , (1) в которой двухместный предикат Р(x, y) определен на множестве MхM, где M={0,1,2,…,n,…}, т.е. MхM=NхN.

В формулу (1) входит переменный предикат P(x,y), предметные переменные x,y,z, две из которых y и z – связанные кванторами, а x – свободная.

Возьмем за конкретное значение предиката P(x,y) фиксированный предикат P⁰(x,y): “x<y”, а свободной переменной х придадим значение . Тогда при значениях y, меньших x⁰=5, предикат P⁰(x⁰,y) принимает значение “ложь”, а импликация при всех принимает значение “истина”, т.е. высказывание 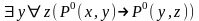имеет значение “истина”.

Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений

Язык логики предикатов удобен для записи математических предложений и определений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства. Приведем несколько примеров таких записей.

Пример 1. Определение предела “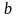 ” функции ƒ(х), определенной в области E, в точке x₀: 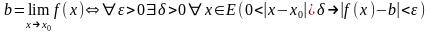. Используя трехместный предикат , запишем: ,

где .

Пример 8. Определение непрерывности функции в точке.

Функция 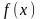, определенная на множестве E, непрерывна в точке 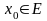, если , где .

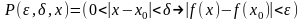Построение противоположный утверждений

Пусть дано некоторое математическое утверждение А. Ему будет противоположным будет утверждение .

Логика предикатов позволяет путем равносильных преобразований формулы придать ей хорошо обозримый вид.

Определение неограниченной функции мы получим, беря отрицание этой формулы и проводя равносильные преобразования: .

Последняя формула дает не негативное, а положительное определение неограниченной функции.

Из приведенного определения видно, что для построения противоположного утверждения к утверждению, заданному формулой логики предикатов, содержащей все кванторы впереди, необходимо заменить все кванторы на противоположные и взять отрицание от предиката, стоящего под знаком кванторов.