Лекция 4. (06.03.12)

Сигнал – источник информации.

- аналоговый

- дискретный

Дискретный сигнал, который дискретизирован по амплитуде, называется цифровым.

Или аналоговый, квантованый по времени и амплитуде.

Совокупность алгоритмов и научных достижений (цифровая обработка сигналов) – часть теории информации.

1965 год – первая работа по обработке цифровых сигналов – Кули, Тьюки.

Математические основы:

1. Классическая математика 17-18 веков

2. Появление компьютеров

3. Достижения микроэлектроники

Цифровая обработка сигналов.

1. Базовые алгоритмы

2. Рациональные способы реализации алгоритмов

3. Алгоритмы решения прикладных задач

Применение: радиолокация, обработка изображений, анализ атомных взрывов, томография и т.д.

Преобразование Фурье:

Х(jw)=

Погрешности:

1. Предел суммирования

2. Из-за замены интеграла суммой

3. Округления

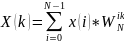
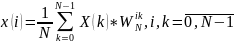
Лекция 5. (13.03.12)

Свойства ДПФ:

1. Линейность

2. Периодичность (X(k)=X(rN+k))

3. Симметрия

4. Теорема Парсеваля

5. Свертка

Физический смысл ДПФ:

Пусть исходная последовательность состоит из действительных чисел.

Оценка числа операций.

Для реальных вычислений используют БПФ со сложностью N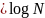

Кули и Тьюки – первая работам по БПФ.

БПФ с прореживанием по времени.

Можно брать по времени и по частоте.

Разреженные мтрицы позволяют сократить число операций.

Итог: если длина массива небольшая, то от БПФ нет смысла, только если надо считать в реальном времени.

Лекция 6. (27.03.12)

Вычисление обратного ДПФ через прямое.

1. X*(k) вместо X(k)

2. ДПФ для X*

3. Результат п2 заменить на комплексно-сопряженные

4. Результат п3 разделить на N

Код Грея

- Такая система кодирования, где 2 соседних значения отличаются только в 1-м разряде:

1) Используются в механических преобразованиях

2) Сведение ошибок к минимуму

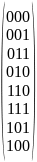
Быстрые алгоритмы применимы для составного значения N

N=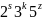

Тут был первый тест.

Лекция 7. (03.04.12)

Минусы Хартли:

1. Его не все знают

2. Преобразование Фурье уже давно используется

3. Коэффициенты Фурье – разложение на cos и sin, а Хартли сдвинут на 45 градусов.

Цифровая интерполяция.

1. Базовые алгоритмы

2. Быстрые алгоритмы

Существуют 3 группы базисных функций.

1. Степенные полиномы

2. Тригонометрические функции

3. Экспотенциальные функции

1. Степенные полиномы:

+наглядность

+удобство дифференцирования и интегрирования

Существует несколько способов интерполяции

1. С узлами

2. С равноотстоящими узлами

3. С неравноотстоящими узлами

4. Методы сплайн-интерполяции (интерполяция кусками)

Ньютон, Стирлинг, Бессель, т. Ролля.

2. Тригонометрические функции (+Фурье)

Бесконечно можно интегрировать и дифференцировать

Недостатки:

1. Пределы суммирования

2. Операции деления---

4. Экспотенциальные функци справедливы лишь в случае выполнении теоремы Котельникова