Лекция 18.

ИНТЕРПОЛИРОВАНИЕ И АППРОКСИМАЦИЯ

§ 18.1. Определение и свойства многочленов Чебышева

Определение 18.1. Многочленом Чебышева называется функция

Т_n (х) := cos(n arccos х), (18.1)

где n  N₀, x  [-1,1].

Прежде всего убедимся, что функция Т_n (х), представленная с помощью тригонометрических функций, на самом деле является многочленом при любом n  N₀.

Непосредственной подстановкой в (18.1) значений п = 0 и п = 1 получаем Т₀ (х) = 1, Т₁ (х) = х.

Положив а := arccos x, имеем:

Т₁ (х) = cos а, Т_n (х) = cos па, Т_n1 (х) = cos(n  1)а, Т_п+1 (х) = соs(n + 1)а,

и так как (по формуле суммы косинусов)

соs(n + 1)а + cos(n  1)а = 2 cos a cos па,

то, значит, справедливо равенство

Т_п+1 (х) + Т_n1 (х) = 2 Т_n (х) Т₁ (х) ,

которое может быть переписано в виде

Т_п+1 (х) + Т_n1 (х) = 2 Т_n (х) Т₁ (х). (18.2)

Формула (18.2) определяет при п = 1, 2, 3,... последовательность функций Т_п(х), начинающуюся с Т₀ (х) = 1, Т₁ (х) = х, рекуррентно; при этом нужно иметь в виду, что здесь x  [-1,1], как и в (18.1).

Подставляя в (18.2) заданные начальные члены последовательности {Т_n (х)}, найдем несколько ее последующих членов:

Т₂(х) = 2х²  1;

Т₃ (х) = 4х³  3х;

Т₄ (х) = 8х ⁴ 8х² +1;

и т.д.

Графики нескольких многочленов Чебышева (с первого по четвертый) изображены на рис.18.1.

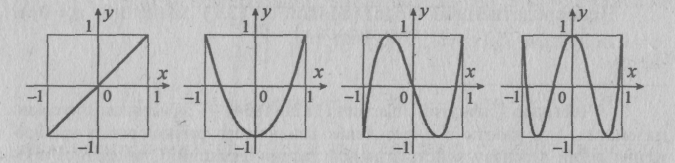
Рис. 18.1.

Анализ рекуррентной формулы (18.2) позволяет считать очевидными следующие факты:

1. все функции Т_n(х), определенные в (18.1), являются многочленами при любом натуральном п;

2. степени этих многочленов возрастают с увеличением п, причем старший член многочлена Т_n(х) равен 2^n1 хⁿ;

3) многочлены Т_n(х) при четных п выражаются через степенные функции только четных степеней, при нечетных — только нечетных.

Наряду с многочленами Чебышева Т_n(х) часто используют многочлены, получаемые из Т_n(х) делением на старший коэффициент, т.е.

— многочлены со старшим коэффициентом 1. Будем называть их нормированными многочленами Чебышева.

Многочлены Чебышева обладают рядом замечательных свойств. Рассмотрим некоторые их свойства, имеющие отношение к поставленной выше проблеме аппроксимации функций.

Свойство 18.1. Многочлен Чебышева Т_n(х) имеет на отрезке [-1,1] ровно п различных действительных корней; все они задаются формулой

, где k = 0,1, ..., п1.

Свойство 18.2. Корни многочленов Чебышева перемежаются с точками их наибольших и наименьших значений, равных соответственно +1 и 1 для Т_n(х), а именно функция Т_n(х), имеет экстремумы Т_n(х_j)= (1)^j в точках

Свойство 18.3 (теорема Чебышева). Из всех многочленов степени п со старшим коэффициентом 1 нормированный многочлен Чебышева Т_n(х) наименее уклоняется от нуля на отрезке [1,1].

§ 18.2. Интерполяция по чебышевским узлам

Вернемся к изучавшейся в предыдущих параграфах задаче интерполяции.

Сравнивая конечноразностные интерполяционные многочлены, построенные по системе равноотстоящих узлов, с интерполяционным многочленом Лагранжа, предполагающим произвольное расположение несовпадающих узлов на промежутке интерполирования [а, b], следует отметить, что первые более просты и удобны в использовании, вторые же обладают большими возможностями. Нет сомнений в том, что если можно располагать узлы в пределах отрезка [а, b] как угодно, то имеет смысл использовать большее количество точечной информации о функции там, где она более сильно изменяется. Особенно существенным это замечание может оказаться при эрмитовой интерполяции.

Подойдем к проблеме расположения узлов интерполяции с несколько иной стороны.

Желая, чтобы интерполяционный многочлен Лагранжа L_n(x) (16.6) в целом хорошо приближал функцию f(x) на отрезке [а, b], поставим вопрос: как расположить на нем n + 1 узлов интерполяции x_i (i = 0,l, ...,n), чтобы при этом минимизировать максимальную на [а, b] погрешность?

Преобразуя формулу (16.8), можно показать, что максимальная погрешность интерполирования достаточно гладкой функции на отрезке [-1, 1] многочленом п–й степени будет минимальной, когда в качестве узлов интерполяции t₀, t₁, ..., …, t_n  [1, 1] берутся корни многочлена Чебышева T_n+1(t). Будем называть их чебышевскими узлами интерполяции.

Если в качестве узлов интерполирования функции f(x) взять точки

где t_i  корни многочлена Чебышева T_n+1(t), то можно получить следующую оценку

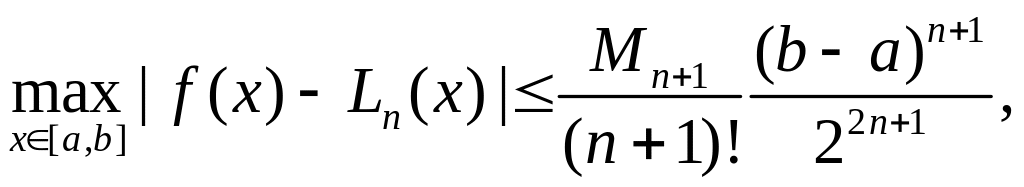(18.3)

Найденная оценка (18.3) называется наилучшей равномерной оценкой погрешности интерполяции.

Можно показать ее неулучшаемость, т.е. что существуют такие функции f(x), для которых нестрогое неравенство (18.3) реализуется в виде равенства.