6. Средние величины, структурные средние (арифметические, геометрические, гармонические формы средней)

Средняя величина обобщает данные о численных значениях изучаемого признака, об отдельных единицах совокупности и определяет типичный уровень признака для единиц этой совокупности в конкретных условиях места и времени. Всегда является именованной. Средняя является результатом абстрагирования от имеющихся у единиц совокупности различий и характеризует то общее, типичное, что присуще всей совокупности в целом. Средние должны исчисляться только для качественно - однородных совокупностей, состоящих из явлений одного рода. Средние, которые применяются в статистике, относятся к классу степенных средних. Общая формула: Из степенных средних в статистике наиболее часто применяется среднее арифметическое (m = 1), реже - среднее гармоническое. При исчислении средних темпов динамики применяется средняя геометрическая:

При исчислении показателей вариации используется среднее квадратическое: (дисперсия).

7. Виды вариации, показатели вариации. Абсолютные и относительные вариации

Вариация – изменения признака от одной единицы совокупности к другой. Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно, по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию. Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей. Абсолютные показатели вариации включают: размах вариации , среднее линейное отклонение , дисперсию, среднее квадратическое отклонение. 1.Размах вариации — это разность между максимальным и минимальным значениями признака. Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности. 2. Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней. ; 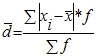- Среднее линейное отклонение взвешенное применяется для сгруппированных данных. 3. Среднее квадратическое отклонение. Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). 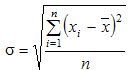Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.Среднее квадратическое отклонение простое: Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных: 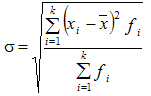Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. 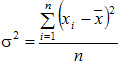Дисперсия простая: Дисперсия взвешенная: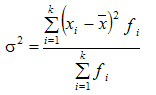 Относительные показатели вариации. Для сравнения вариации в разных совокупностях рассчитываются относительные показатели вариации. К ним относятся коэффициент вариации, коэффициент осцилляции и линейный коэффициент вариации (относительное линейное отклонение). Коэффициент вариации – это отношение среднеквадратического отклонения к среднеарифметическому, рассчитывается в процентах: Коэффициент вариации позволяет судить об однородности совокупности: – < 17% – абсолютно однородная; – 17–33%% – достаточно однородная; – 35–40%% – недостаточно однородная; – 40–60%% – это говорит о большой колеблемости совокупности. Коэффициент осцилляции – это отношение размаха вариации к средней, в процентах. Отражает относительную колеблемость крайних значений признака вокруг средней. Линейный коэффициент вариации характеризует долю усредненного значения абсолютного отклонения от средней величины. Виды вариации: 1) дискретная – называется вариация, при которой одно значение признака отличается от другого на конечную величину. 2) непрерывная – называется вариация, при которой признак может принимать любые значения в некотором ограниченном интервале с соответствующей вероятностью. При непрерывной вариации строится интервальный ряд распределения(ряд варьирующего элемента).