
- •1. Два подхода к формированию понятия «архитектура компьютера»
- •Вопрос 2. Архитектура фон неймана: принципы, проблемы и способы их решения
- •7. Графический процессор
- •Вопрос 3. Типы команд и техника (методы) адресации
- •Вопрос 4. Иерархия памяти: регистровая, кэш, оперативная главная и вспомогательная
- •Вопрос 5. Организация кэш-памяти.
- •Вопрос 8. Семантический разрыв между архитектурными решениями компьютеров и его программным окружением
- •Вопрос 9. Компьютеры в режиме управления технологическим процессом
- •Вопрос 10. Cisc- и risc-архитектуры
- •Вопрос 11. Компьютеры со стековой архитектурой
- •Вопрос 12: нейрокомпьютеры
- •14. Процессоры с микропрограммным управлением.
- •Вопрос 15. Методы повышения эффективности функционирования компьютеров
- •16. Многоядерный процессор
- •Вопрос 21. Ортогональная память. Вс с комбинированной структурой.
- •Вопрос 17. Организация системы прерываний.
- •Вопрос 18. Vliw-архитектура.
- •19. Конвейеризация. Predication и speculation. Конвейерные системы.
- •Вопрос 20. Матричные компьютеры.
- •Вопрос 23. Топологии локальных сетей
- •Вопрос 24. Архитектура программного обеспечения.
- •Вопрос 31. Классификация ошибок. Программные методы контроля ошибок
- •Вопрос 32. Управление процессами в многопроцессорных и однопроцессорных компьютерах
- •Вопрос 33. Информационные модели систем параллельногодействия: мультипроцессоры и мультикомпьютеры.
- •Вопрос 35. Программное обеспечение для мультикомпьютеров.
- •Вопрос 37. Алгоритмы выбора маршрутов для доставки сообщений.
- •Вопрос 39. Основные подходы к проектированию языков параллельного программирования
- •40. Языки параллельного программирования.
- •Вопрос 41. Преобразование последовательных программ в последовательно-параллельные
- •Вопрос 42. Планирование в мультисистемах.
- •25. Кодирование данных с симметричным представлением цифр.
- •26. Кодирование данных в системах с отрицательным основанием.
- •30 Алгоритм деления в системе с отрицательным основанием.
- •27 Кодирование данных с помощью вычетов.
- •13. Искусственные нейронные сети. Обучение сетей.
26. Кодирование данных в системах с отрицательным основанием.
Известны
компьютеры, работающие в СКД с
отрицательными основаниями.
Целесообразность введения отрицательного
основания обусловливается тем, что
знак числа органически включается в
представление числа, в связи с чем
специально его отображать не надо.
Известно, что каждое целое число A может
быть представлено в виде
![]() .
где
при n < –1 имеет место 0 . Ci <
–n–1.
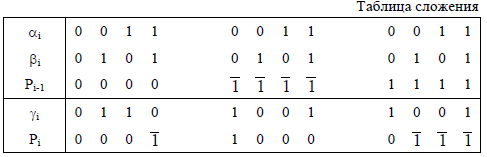
Рассмотрим наиболее привычный
случай СКД при n = –2. Здесь Ci . {0; 1}.
Предположим, что m = 5. Тогда таблица
представления целых чисел от –10 до 10
будет иметь следующий вид (табл. 1).
.
где
при n < –1 имеет место 0 . Ci <
–n–1.
Рассмотрим наиболее привычный
случай СКД при n = –2. Здесь Ci . {0; 1}.
Предположим, что m = 5. Тогда таблица
представления целых чисел от –10 до 10
будет иметь следующий вид (табл. 1).
 Из
табл. 5.1 видно, что знак числа определяется
местоположением первой значащей цифры:
если старшая значащая цифра стоит в
четном разряде, число отрицательное,
если в нечетном – положительное.
Из
табл. 5.1 видно, что знак числа определяется
местоположением первой значащей цифры:
если старшая значащая цифра стоит в
четном разряде, число отрицательное,
если в нечетном – положительное.

 2.
Вычитание. Так как a-b = a+b-2b = a+b+b(-2), причем
b(-2) – это число b, сдвинутое на один
разряд влево, то алгоритм вычитания
может быть сформулирован так. Для того
чтобы из a вычесть b, необходимо к a
прибавить b и прибавить b, сдвинутое на
один разряд влево.
3. Умножение
Операция умножения осуществляется
посредством последовательных сложений
и сдвигов.
2.
Вычитание. Так как a-b = a+b-2b = a+b+b(-2), причем
b(-2) – это число b, сдвинутое на один
разряд влево, то алгоритм вычитания
может быть сформулирован так. Для того
чтобы из a вычесть b, необходимо к a
прибавить b и прибавить b, сдвинутое на
один разряд влево.
3. Умножение
Операция умножения осуществляется
посредством последовательных сложений
и сдвигов.

30 Алгоритм деления в системе с отрицательным основанием.

![]()
28.
ПОМЕХОЗАЩИТНЫЕ КОДЫ. КОД ХЭММИНГА
Код
Хэмминга позволяет автоматически
исправлять ошибки, возникающие в
отдельных кодовых словах.
Это,
в частности, необходимо при хранении
данных в полупроводниковой памяти.
Возникающие здесь ошибки появляются
в различных разрядах независимо, а это
значит, что вероятность однократной
ошибки на несколько порядков выше, чем
двукратной, трехкратной и т.д.
Общая
схема кодирования – декодирования по
Хэммингу показана на рис.9.1.
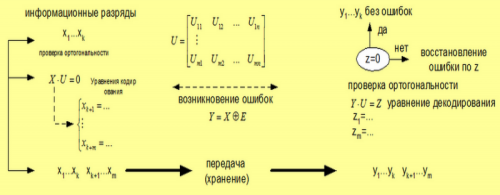
При
кодировании передаваемые
информационные разряды х1 ..хк дополняются
m избыточными разрядами таким образом,
чтобы полученный кодовый вектор Х
{х1…хn} отвечал условию ортогональности
некоторой проверочной матрице, состоящей
из m строк.
В
развернутом виде запись условия
ортогональности выглядит как система
из m уравнений вида ![]()
(здесь j = 1,m – номер проверочного уравнения). Собственно процедура кодирования как раз и состоит в нахождении проверочных разрядов хк+1…хк+m по m уравнениям ортогональности (формула 9.2).В ходе передачи данных (напомним, что хранение в памяти интерпретируется как передача во времени) могут возникнуть ошибки. Удобно представить совокупность ошибок при передачи слова Х как вектор E, содержащий “1” в неверных разрядах. Тогда принятый кодовый вектор Y в общем случае отличается от переданного. Декодирование означает проверку правильности вектора Y и исправление ошибки, если она обнаружена. С этой целью вектор Y {y1…yn} вновь проверяется на ортогональность той же матрице (здесь вектор , если произошла ошибка). Замечательное свойство кода Хэмминга состоит в том, что по виду вектора Z можно определить не только наличие ошибки, но и номер разряда, в котором она произошла, а значит – исправить ее инвертированием). Напомним, что для исправления однократной ошибки необходимо Именно такое значение обеспечивается за счет выбора m в коде Хемминга.
