Лабораторная работа №5

Исследование резонанса токов.

Цель работы. Изучение и экспериментальное исследование явления резонанса токов.

Основные теоретические сведения.

Резонансом называется такой режим электрической цепи, при котором входной ток совпадает по фазе с входным напряжением, несмотря на наличие в цепи реактивных элементов.

Резонансный режим наступает тогда, когда частота внешних воздействий на систему равна собственной частоте системы

ω = 2πƒ = ω_о = 2 πƒ_о, (4.1)

т.е. частоте преобразования энергии внутри системы из одной формы в другую (энергии магнитного поля в энергию электрического поля и наоборот). Резонанс, таким образом, возникает при нали­чии в цепи индуктивности и емкости.

Одна из ценных особенностей резонансов - это значительное увеличение напряжений или токов при весьма экономичном использовании электрической энергии.

Резонанса в электрической цепи можно достичь, изменяя либо частоту источника питания, либо индуктивность, либо емкость.

Цепь, находящаяся в резонансном режиме, характеризуется следующим:

1) входные реактивные сопротивления или проводимости равны нулю:

χ _вx =0; b_вx =0;

2) угол сдвига фаз между входным током и входным напряжением равен нулю, а коэффициент мощности максимален:

φ_вx =0; Cosφ _вx =1;

3) входная мощность чисто активная:

Ŝ_вx =P_вx ±jQ _вx =P_вx

Резонанс токов.

Резонанс при параллельном соединении индуктивности и емкости, при взаимной компенсации реактивных составляющих токов в параллельных ветвях, называют резонансом токов.

Если к цепи, изображенной на рис. 4-1, приложено переменное синусоидальное напряжение

, (4.2)

то ток равен

, (4.3)

где

, , .

Из приведенного выражения видно, что ток будет совпадать с приложенным напряжением при условии b =0 или

, т.е. (4.4)

Таким образом, при резонансе токов входная реактивная проводимость цепи b_вx равна нулю, а полная проводимость У имеет на­именьшее значение, поэтому ток в неразветвленной части цепи минимален.

При резонансе токов в параллельных ветвях реактивные составляющие токов равны между собой:

I_L =I_C

и могут во много раз превышать ток в неразветвленной части цепи, что характеризуется величиной добротности :

, (4.5)

где

^, (4.6)

ρ - волновое или характеристическое сопротивление контура.

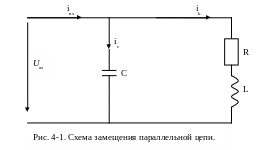
В екторная диаграмма резонанса токов в цепи (рис. 4-1.) имеет вид:

Нерезонансные режимы.

Р ежимы вне резонанса можно получить, если вывести систему из резонанса, т.е. нарушить условие (14.1), изменяя собственную частоту контура с помощью индуктивности L при постоянной емкости С , или изменяя емкость С при постоянной индуктивности L. В результате этой операции можно получить частотные характерис­тики (рис. 4-3 и рис. 4-4).

С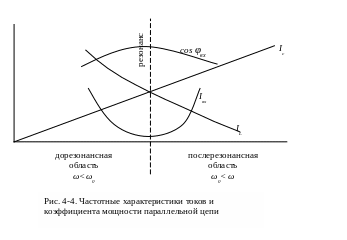 ледует отметить, что частотные характеристики параллельной цепи обратны по отношению к частотным характеристикам последовательной цепи, это происходит потому, что параллельное соединение элементов является обратным последовательному соединению. Остро­та частотных характеристик зависит от добротности цепи . Чем выше значение добротности, тем более острыми получаются пики кривых и лучше избирательные качества цепи.

Изменяя величину емкости конденсатора при постоянной индуктивности можно получить графики функциональных зависимостей в параллельной цепи (рис. 4-5) и построить соответствующие векторные диаграммы (рис. 4-6).

Для схемы рис. 4-1 на основании векторных диаграмм для нерезонансных режимов (рис. 4-6) можно построить треугольник токов для всей цепи (рис. 4-7,а), а также для отдельной ветви, в дан­ном случае для ветви с катушкой (рис. 4-7,6). Для этой же ветви построен треугольник сопротивлений на рис. 4-7,в.

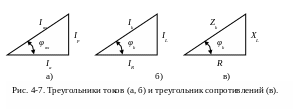
В схеме рис.4-1 активная составляющая входного тока определяется активной составляющей тока катушки I_R. Если сопротивление ветви с катушкой не изменяется, то I_R=const, а, следовательно, и =const.

Из треугольников рис.4-7 следует:

; (4.7)

;

.

Следовательно,

. (4.8)

Перечень оборудования:

1. Источники переменного напряжения 220В, 35В, ƒ =50Гц.

2. Катушка индуктивности с ферромагнитным сердечником с подмагничиванием (подмагничивание постоянным током уменьшает эквивалентную индуктивность катушки).

3. Батарея конденсаторов со ступенчатым регулированием 94 мкФ.

4. Вольтметр 100 В.

5. Амперметры - 3 шт. с пределом измерений 2 А.

Содержание работы.

Исследовать дорезонансный, резонансный и послерезонансный режимы параллельной цепи изменением индуктивности при постоянной емкости и изменением емкости при постоянной индуктивности. Измерить параметры катушки при помощи амперметра, вольтметра и ваттметра.

Порядок выполнения работы.

1.Собрать схему для исследования параллельной цепи (рис.4-8)

2.Ключ В1 замкнут. Включаем выключатели батареи конден­саторов, набираем суммарную емкость С=30 мкФ. Включаем источники питания тумблерами. Изменяя индуктивность катушки, устанавливаем резонансный режим, который определяется по минимальному показанию амперметра . Показания приборов занести в таблицу I.

3.Изменяя индуктивность катушки, установить дорезонансный режим ( уменьшается), затем послерезонансный режим ( увеличивается). Показания приборов для одной точки дорезонансного режима и одной точки послерезонансного режима занести в таблицу 1.

Таблица 1

Режимы цепи	Данные измерений
	Uвх,В	Р, Вт	Iвх, А	Iс, А	Iк, А
Резонанс Дорезонансный Послерезонансный

4. По данным таблицы 1 построить векторные диаграммы цепи для трех режимов: резонансного, дорезонансного и послерезонансного.

Диаграмму удобно строить методом засечек с помощью циркуля, согласно балансу токов .

5. Установить ток , близкий к резонансному, регулированием индуктивности (рукоятка L). Разомкнуть ключ В1, показания приборов занести в таблицу 2.

Таблица 2

Данные измерений			Данные вычислений
Uвх,В	Iвх, А	Р, Вт	Rк, Ом	Z, Ом	Xi,Ом	Lк, Гн

6. По данным таблицы. 2 определить по формулам:

; ; ; ; (4.9)

7. Включить суммарную емкость С=30 мкФ. Ключ В1 замкнуть. Изменяя индуктивность, установить резонансный режим, Оставив индуктивность неизменной, записать показания приборов при ступенчатом изменении емкости в пределах имеющегося магазина емкостей. Показания приборов занести в таблицу 3.

Таблица 3

№ п/п	Данные измерений						Данные вычислений
	С,мкФ	Uвх,В	Iвх,А	Iс, А	Iк, А	Р, Вт	Cosφвх	Z, Ом	Qg
1 2 3 4 5 6

8. По данным таблицы 3 построить графики зависимостей:

определяется из соотношения (4.7); из соотношения (4.5).

Содержание отчёта.

Отчет должен содержать:

1.Название работы.

2.Цель работы.

3.Схема исследования.

4.Таблица приборов и оборудования.

5.Таблицы с результатами измерений и вычислений.

6.Расчетные формулы.

7.Графики зависимостей.

8.Векторные диаграммы.

9.Выводы об особенностях резонансного и нерезонансного режимов.

Контрольные вопросы.

1.Что такое резонанс токов?

2.Каким способом регулируется собственная частота цепи?

3. Чем определяется величина усиления токов?

4.Почему входной коэффициент мощности при резонансе равен единице, а до и после резонанса быстро снижается?

5.Как строятся векторные диаграммы цепи для режимов до и после резонанса, для режима резонанса?

6.Почему резонансные режимы весьма экономичны?

7.Где используются резонансы токов?

Литература

1. Электротехника/ Под ред. В.С. Пантюшина.- М.: Высшая школа, 1976, гл. 5, С.116-119. •

2. Касаткин А.С., Немцов М.В.,. Электротехника.- М.: Енергоатомиздат, 1983, гл. 2, С.84-86, 97-98.

3. Бессонов Л.А.Теоретические основы электротехники. -М.: Высшая школа,1984,§3.26,3.27.