Поэтому

В момент времени t₁ = 2 с имеем

s₁ = AB₁ = 20 cм, V_отн = 3 см/с, а_отн =  6 см/с². (67)

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния s, а вектор – в противоположную сторону. Изображаем эти векторы на рис. К3б.

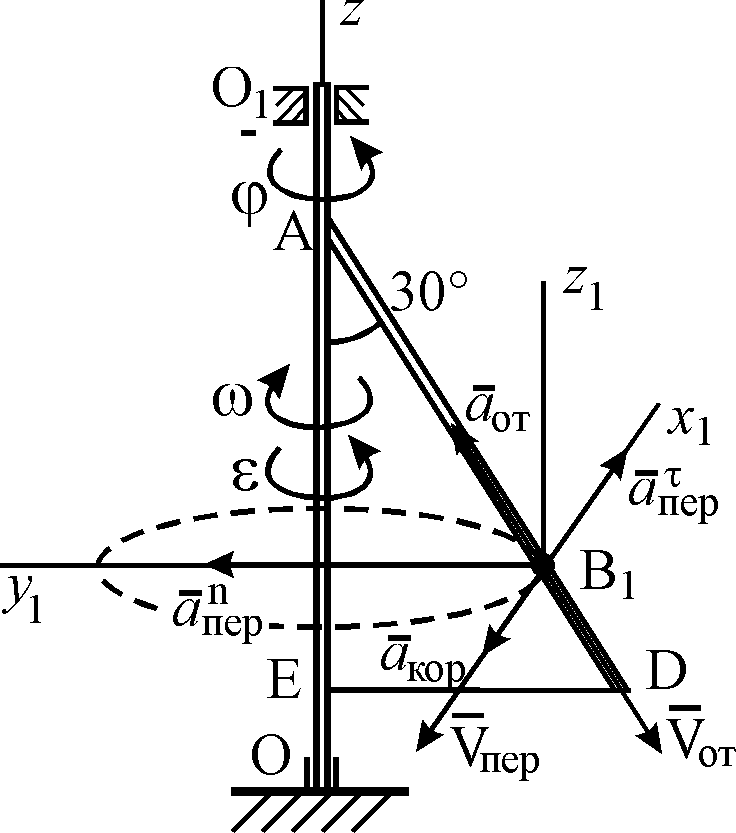
Рис. К3б

2. Переносное движение. Это движение (вращение) происходит по закону  = 0,1t³  2,2t.

Найдем угловую скорость  и угловое ускорение  переносного вращения:  = = 0,3t²  2,2;  = = 0,6t и при t₁ = 2 с,

 =  1 c^1,  = 1,2 c^2. (68)

Знаки указывают, что в момент t₁ = 2 с направление  совпадает с направлением положительного отсчета угла , а направление  ему противоположно; отметим это на рис. К3б соответствующими дуговыми стрелками.

Из рисунка находим расстояние h₁ точки В₁ от оси вращения z: h₁ = AB₁ sin 30° = 10 см. Тогда в момент t₁ = 2 с, учитывая равенства (68), получаем:

V_пер = ||h₁ = 10 cм/с,

= ||h₁ = 12 см/с², = ²h₁ = 10 см/с². (69)

Изобразим на рис. К3б векторы и (с учетом знаков  и ) и ; направлены векторы и перпендикулярно плоскости ADE, а вектор – по линии В₁С к оси вращения.

3. Кориолисово ускорение. Так как угол между вектором и осью вращения (вектором ) равен 30°, то численно в момент времени t₁ = 2 с

а_кор = 2|V_отн|  ||  sin 30° = 3 см/с². (70)

Направление найдем по правилу Н. Е. Жуковского. Для этого вектор спроецируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору ) и затем эту проекцию повернем на 90° в сторону , т. е. по ходу часовой стрелки; получим направление вектора . Он направлен перпендикулярно плоскости пластины так же, как вектор (см. рис. К3б).

4. Определение V_абс. Так как = + , а векторы и взаимно перпендикулярны, то ; в момент времени t₁ = 2 с V_абс = 10,44 см/с.

5. Определение а_абс. По теореме о сложении ускорений

= + + + . (71)

Для определения а_абс проведем координатные оси В₁хуz₁ и вычислим проекции на эти оси. Учтем при этом, что векторы и лежат на оси х₁, а векторы и расположены в плоскости В₁хуz₁, т. е. в плоскости пластины. Тогда, проецируя обе части равенства (71) на оси В₁хуz₁ и учтя одновременно равенства (67), (69), (70), получаем для момента времени t₁ = 2 с:

а_{абс х} = | | – а_кор = 9 см/с²,

а_{абс у} = + |а_отн|sin 30 ° = 13 см/с²,

а_{абс z} = |а_отн|cos 30 ° = 5,20 см/с².

Отсюда находим значение а_абс:

см/с².

Ответ: V_абс = 10,44 см/с, а_абс = 16,64 см/с².

Вопросы для самоконтроля

1. Что понимается под составным (сложным) движением точки?

2. Что называется абсолютным, переносным и относительным движением точки?

3. Сформулируйте, что такое переносная скорость и переносное ускорение точки.

4. В чем заключается теорема об абсолютной скорости точки, совершающей составное движение.

5. Сформулируйте теорему об ускорениях точки в составном движении.

6. Как определить модуль и направление кориолисова ускорения точки?

7. В каких случаях ускорение Кориолиса равно нулю?