
- •Определение систем в рамках теоретико - множественного подхода. Математические модели простых динамических систем.
- •Принцип разделения в цифровых системах управления. Обоснование для линейно – квадратичной задачи управления в дискретном времени.
- •Решение задачи линейного программиро-вания на основе симплекс- метода.
- •Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Теорема о нормальной корреляции и ее следствия.
- •Классификация систем управления. Основ-ные этапы синтеза сложных систем управления.
- •Метод анализа иерархий.
- •Устойчивость динамических систем. Теорема Ляпунова в непрерывном и дискретном времени.
- •Иерархическая схема управления сложным объектом. Основные принципы иерархического управления.
- •Управляемость и наблюдаемость систем управления.
- •Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Постановка и пример задачи автоматичес-кого управления для непрерывных динамичес-ких систем. Задачи Больца, Лагранжа, Майера.
- •Метод анализа иерархий.
- •Общее решение задачи автоматического управления без ограничений для детерминиро-ванной системы на основе методов вариации-онного исчисления.
- •Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Управление ресурсами и задача линейного программирования. Примеры, геометрическая интерпретация.
- •Решение задачи линейного программиро-вания на основе симплекс – метода.
- •Теорема о нормальной корреляции и ее следствия.
- •Решение задачи линейного программиро-вания на основе симплекс – метода
- •2.Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Синтез структуры сложной системы управления. Метод ветвей и границ.
- •Принципы координации в задачах управления сложными объектами.
- •2. Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Метод анализа иерархий.
- •2. Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Общее решение задачи автоматического управления без ограничений для детерминированной системы на основе методов вариационного исчисления.
- •2. Оптимальное управление в стохастических системах. Принцип разделения в непрерывных стохастических системах.
- •Принципы координации в задачах управления сложными объектами.
- •2. Уравнения фильтра Калмана в дискретном времени. Пример постановки задачи стохастического управления (управление нефтехранилищем).
- •Синтез структуры сложной системы управления. Метод ветвей и границ.
- •2. Принцип максимума Понтрягина и решение задачи о быстродействии при переводе материальной точки в начало координат.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Решение задачи о пошаговом распределении ресурсов на основе принципа оптимальности Беллмана.
- •Принцип максимума Понтрягина и решение задачи о быстродействии (задача о «лифте»).
- •2. Применение микропроцессоров и микро – эвм в цифровых системах управления.
Устойчивость динамических систем. Теорема Ляпунова в непрерывном и дискретном времени.
Устойчивость.
Пусть,
например, система определяется
отображением
 где
d
и e
соответствуют причине и следствию
некоторого явления. Причинно-следственная
пара (d,e)
называется устойчивой, если незначительные
отклонения от e
вызываются малыми отклонениями от d,
т.е. для всех
где
d
и e
соответствуют причине и следствию
некоторого явления. Причинно-следственная
пара (d,e)
называется устойчивой, если незначительные
отклонения от e
вызываются малыми отклонениями от d,
т.е. для всех
 ,
близких
к d
,
близких
к d
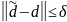 ,
соответствующие
следствия
,
соответствующие
следствия
 будут близки к e,
будут близки к e,
 ,
где
,
где
 – малые величины, причем величина
– малые величины, причем величина
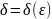 связана с
связана с .
Это означает, что малые
отклонения d
не могут существенно изменить следствие.
Пусть
имеется уравнение
.
Это означает, что малые
отклонения d
не могут существенно изменить следствие.
Пусть
имеется уравнение
 описывающее
поведение системы в евклидовом
пространстве X,
для которого в некоторой области
описывающее
поведение системы в евклидовом
пространстве X,
для которого в некоторой области
 выполнены условия существования и
единственности решения. Управление в
обозначим в форме функции f(…).
выполнены условия существования и
единственности решения. Управление в
обозначим в форме функции f(…).
Теорема
Ляпунова.
Решение
 называется устойчивым по Ляпунову,
если для любого
называется устойчивым по Ляпунову,
если для любого
 существует такое
существует такое
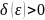 ,
что для любого
,
что для любого
 ,
удовлетворяющего условию
,
удовлетворяющего условию
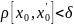 ,
,
 при всех t>0.
Здесь
при всех t>0.
Здесь
 – некоторая метрика в евклидовом
пространстве, например, «модуль».
Другими словами, устойчи-вость по
Ляпунову означает равномерно непре-рывную
зависимость решений от начальных
данных.
Если
требуют дополнительно, чтобы выполнялось
– некоторая метрика в евклидовом
пространстве, например, «модуль».
Другими словами, устойчи-вость по
Ляпунову означает равномерно непре-рывную
зависимость решений от начальных
данных.
Если
требуют дополнительно, чтобы выполнялось
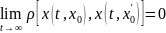 ,
то подобное поведение системы называют
асимптоти-ческой устойчивостью.
Вещественную
непрерыв-но
дифференцируемую и знакопостоянную
функцию
,
то подобное поведение системы называют
асимптоти-ческой устойчивостью.
Вещественную
непрерыв-но
дифференцируемую и знакопостоянную
функцию
 ,
удовлетво-ряющую
условию
,
удовлетво-ряющую
условию
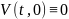 ,
называют функцией Ляпунова.
,
называют функцией Ляпунова.
Теорема
(первая теорема Ляпунова). Пусть
существует функция Ляпунова
 такая, что
такая, что
 ,
где
,
где

 – скалярная непрерывная неубывающая
функция такая, что
– скалярная непрерывная неубывающая
функция такая, что
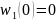 и
,
и
,
 .
Пусть также
.
Пусть также
 ,
где
,
где
 – называется производной функции
Ляпунова в силу системы.
– называется производной функции
Ляпунова в силу системы.
Возьмем
 и любое
и любое
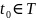 .
В качестве
.
В качестве
 выберем такое число, что
выберем такое число, что
 ,
,
 .
Из непрерывности V(t,x)
и условия V(t,0)=0
следует, что такое число найдется.
Условие
.
Из непрерывности V(t,x)
и условия V(t,0)=0
следует, что такое число найдется.
Условие
 означает, что функция V(t,x)
не возрастает вдоль решений исходного
уравнения. При
означает, что функция V(t,x)
не возрастает вдоль решений исходного
уравнения. При
 и
и
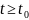 ,
получим
,
получим
 ,
.
В силу монотонности
отсюда вытекает, что
,
.
В силу монотонности
отсюда вытекает, что
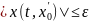 .
Нахождение
функций Ляпунова позволяет исследовать
уравнения на устойчивость без их
решения.
.
Нахождение
функций Ляпунова позволяет исследовать
уравнения на устойчивость без их
решения.
И нтерпретация
задачи определения устойчивости для
системы, описываемой конечно-разностным
уравнением в дискретном времени
нтерпретация
задачи определения устойчивости для
системы, описываемой конечно-разностным
уравнением в дискретном времени
 .
Функция
.
Функция
 является функцией Ляпунова для системы
в случае если
является функцией Ляпунова для системы
в случае если
1.
 непрерывна по X
и
непрерывна по X
и
 ;
;
2.
 – положительно определена при
– положительно определена при
 ;
;
3.
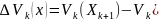 (неотрицательно определена).
(неотрицательно определена).
Теорема
об устойчивости формулируется следующим
образом: если для системы
существует функция Ляпунова, то решение
 асимптотически устойчиво. Функция
Ляпунова легко определяется для линейных
систем вида
асимптотически устойчиво. Функция
Ляпунова легко определяется для линейных
систем вида
 .
.
Разность
 для
другого решения
для
другого решения
 также
удовлетворяет уравнению
также
удовлетворяет уравнению
 .
Это
значит, что если
устойчиво, то каждое другое решение
также устойчиво. То есть для линейных
систем устойчивость – свойство системы,
а не конкретного решения.Для линейной
системы при a=0
функцию Ляпунова обычно ищут в виде
.
Это
значит, что если
устойчиво, то каждое другое решение
также устойчиво. То есть для линейных
систем устойчивость – свойство системы,
а не конкретного решения.Для линейной
системы при a=0
функцию Ляпунова обычно ищут в виде
 где
B
– положительно определенная матрица.
Вычислим первую разность функции
Ляпунова и преобразуем ее к виду
где
B
– положительно определенная матрица.
Вычислим первую разность функции
Ляпунова и преобразуем ее к виду
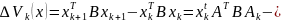
 ,
где C
– некоторая положительно определенная
матрица, которая находится из матричного
уравнения
,
где C
– некоторая положительно определенная
матрица, которая находится из матричного
уравнения
 .
Это уравнение (матричное уравнение
Ляпунова) всегда имеет решение, если
система устойчива. В качестве C
обычно выбирают единичную матрицу(C=I).
Если матрицу A
путем невырожденного преобразования
F
можно привести к диагональному виду,
то
.
Это уравнение (матричное уравнение
Ляпунова) всегда имеет решение, если
система устойчива. В качестве C
обычно выбирают единичную матрицу(C=I).
Если матрицу A
путем невырожденного преобразования
F
можно привести к диагональному виду,
то

 и
решение есть линейная комбинация
и
решение есть линейная комбинация
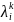 ,
где
,
где
 ,
,
 собственные числа A.
Для достижения асимптотической
устойчивости все решения должны
стремиться к нулю при
собственные числа A.
Для достижения асимптотической
устойчивости все решения должны
стремиться к нулю при
 .
В этом случае все собственные числа A
должны обладать свойством
.
В этом случае все собственные числа A
должны обладать свойством
 .
В самом простейшем случае скалярного
уравнения
.
В самом простейшем случае скалярного
уравнения
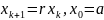 устойчивость достигается при
устойчивость достигается при
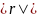 <1,
так как
<1,
так как
 и любое возмущение начального значения
будет «погашено» с течением времени.
и любое возмущение начального значения
будет «погашено» с течением времени.
