2. Теорема о нормальной корреляции и ее следствия.

Теорема. Для гауссовских векторов оптималь-ная оценка в виде условного среднего вектора относительно ξ (по наблюдению ξ) и ее матрица ошибок задаются формулами

= , , ,

,

.

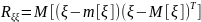Доказательство. Образуем вектор

.

,то есть вектор η не коррелирован с вектором . В силу гауссовости векторов и вектор , а также η будут гауссовскими. Некоррелированность для гауссовских векторов означает их независи-мость. Значит η и ξ-M[ξ], а также η и ξ будут независимы и, следовательно, M[η/ξ]=M[η] 0.

Следует, что . Для доказательства выражения для матрицы ковариации ошибок рассмотрим условную ко-вариацию . Поскольку 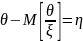, то, в силу независимости η и ξ.

Поскольку 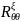не зависит от случая, то есть от наблюденийξ, то .Теорема доказана в целом.

1. Если величины и ξ некоррелированы, то есть ,тогда , , Наблюдение за ξ не дает новой информации относительно значений .

2. Если величины и ξ полностью коррелированы, то есть , , то

. Наблюдение за ξ дает полную информацию о .

Следствие 1.Пусть и ξ случайные векторы, а G – некоторая совокупность условий. Тогда

=

.

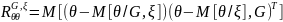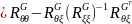
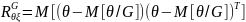
Следствие 2.

Обозначим векторы ,

,

, . Тогда с учетом первого следствия .

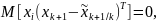
Оценка является линейной и ее можно представить в виде – некоторые известные коэффициенты. Тогда

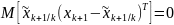. Данное следствие носит название леммы об ортогональном проецировании и свидетельствуют о том, что ошибка оценивания ортогональна в статистическом смысле любому из наблюдений.

Контрольно-измерительный материал № 4

1. Классификация систем управления. Основ-ные этапы синтеза сложных систем управления.

Классификация СУ может осуществляться различным образом. Прежде всего, она осуществля-ется по задачам или целям управления. В СУ ре-шаются обычно задачи четырех типов (стаби-лизация, выполнение программы, слежение, оптимизация).

Задача стабилизации объекта управления состоит в поддержании его выходных параметров (состояний) вблизи некоторых заранее известных значений, несмотря на действие помех и различного рода возмущений.

Задача выполнения программы возникает в случаях, когда значения управляемых величин должны изменяться во времени по заранее заданному закону, который не может быть изменен в процессе движения и фактически не зависит от состояния объекта.

Задача слежения при управлении объектами соответствующего типа состоит в установлении как можно более точного соответствия между текущим состоянием управляемой системы и состоянием другой системы.

Задача оптимизации состоит в том, чтобы наилучшим образом в смысле заданного критерия достичь поставленной цели при реальных условиях и ограничениях. Понятие оптимальности каждый раз конкретизируется.

По степени участия человека в процессе управления системы управления делятся на два больших класса: системы автоматического управления (САУ) и автоматизированные системы управления (АСУ).

Основные задачи, решаемые САУ, относятся к задачам стабилизации, выполнения программы.

В АСУ в контур управления включен человек, на которого возлагаются функции принятия важных решений и ответственность за принятые решения. \

Классификация СУ и, прежде всего, АСУ проводится также и по особенностям структуры их построения следующим образом.

1. По числу уровней иерархии системы делятся на многоуровневые и одноуровневые. Многоуровневые СУ могут быть однородными и неоднородными.

2. По принципам управления и подчиненности системы делятся на централизованные, децентрализованные и смешанные.

3. По возможности изменения структуры во времени различают системы с жесткой (фиксированной) структурой и системы с переменной (адаптивной) структурой.

4. По принципам разбиения элементов системы на подсистемы классифицируют структуру систем, в которых элементы объединяются по функциональному и (или) объектному принципам. В организационных СУ при этом различают линейную, функциональную и линейно-штабную структуры управления.

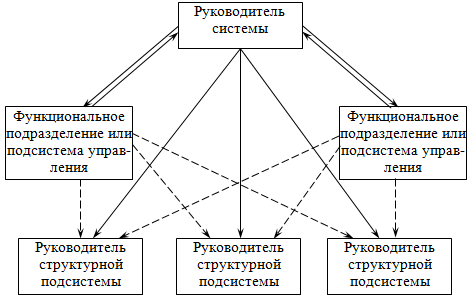
Важнейшим принципом классификации систем управления является их разделение на простые и сложные. Формализация процессов и синтез управления в простой системе осуществляются на основе существующей методологии теории автоматического управления (регулирования).

Создание сложной СУ предусматривает рассмотрение нескольких этапов ее построения. Факторы сложности объекта управления:

• отсутствие законченного математического описания;

• стохастический характер поведения;

• развивающийся характер поведения;

• негативность к управлению;

• невоиспроизводимость в эксперименте

Особенности процесса создания сложной СУ часто приводят к тому, что цель управления таким объектом в полной мере никогда не достигается

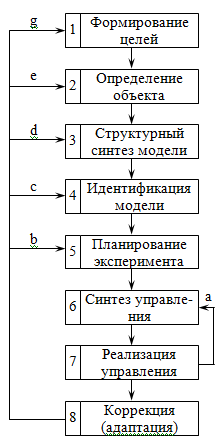
1. Формирование целей управления. Определение совокупности целей явля-ется наименее формали-зуемым этапом. Оно базиру-ется на реализации различ-ного рода методов систем-ного анализа и эвристичес-ких приемах для определе-ния целевых функций и по-казателей качества управле-ния.

2. Определение объекта. Этот этап связан с выделе-нием той части среды, состояние которой субъект может изменить в выгодном для себя направлении.

3. Структурный синтез модели. Модель F, связывающая входы X и U с выходом объекта Y, определяется структурой W и параметрами H F=(W,H). Этап структурного синтеза модели включает: определение внешней структуры; декомпозицию модели; определение внутренней структуры.

Синтез внешней структуры сводится к содержательному определению входов X и U и выхода Y без учета внутренней структуры.

Декомпозиция модели заключается в том, чтобы на основе априорных сведений об объекте, упростить задачу синтеза структуры модели путем выделения основных функциональных действий или функциональных подсистем, определяющих поведение объекта.

4. Идентификация параметров модели. Этот этап состоит в определении числовых характеристик H в режиме нормального функционирования объекта.

5. Планирование эксперимента. Данный этап направлен на осуществление синтеза плана эксперимента, позволяющего с максимальной эффективностью определить искомые характеристики модели объекта управления.

6. Синтез управления. На этом этапе принимается решение о том, каково должно быть управление U*, чтобы достичь заданной цели управления Z*.

7. Реализация оптимального управления или отработка оптимального решения U*, полученного на предыдущем этапе. Реализовав управление и убедившись, что цель управления не достигнута, возвращаются к одному из предыдущих этапов. В случае, когда цель управления достигнута, необходимость обращения к предыдущему этапу вызывается изменением только состояния среды X.

8. Коррекция (адаптация). Специфика управления сложной системой состоит в том, что вследствие наличия помех и нестационарности информация, полученная на предыдущих этапах, только приближенно отражает состояние системы в текущий момент времени. Это вызывает необходимость коррекции ранее полученных результатов. Коррекция может затрагивать различные этапы, вплоть до изменения целей управления.