
- •Определение систем в рамках теоретико - множественного подхода. Математические модели простых динамических систем.
- •Принцип разделения в цифровых системах управления. Обоснование для линейно – квадратичной задачи управления в дискретном времени.
- •Решение задачи линейного программиро-вания на основе симплекс- метода.
- •Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Теорема о нормальной корреляции и ее следствия.
- •Классификация систем управления. Основ-ные этапы синтеза сложных систем управления.
- •Метод анализа иерархий.
- •Устойчивость динамических систем. Теорема Ляпунова в непрерывном и дискретном времени.
- •Иерархическая схема управления сложным объектом. Основные принципы иерархического управления.
- •Управляемость и наблюдаемость систем управления.
- •Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Постановка и пример задачи автоматичес-кого управления для непрерывных динамичес-ких систем. Задачи Больца, Лагранжа, Майера.
- •Метод анализа иерархий.
- •Общее решение задачи автоматического управления без ограничений для детерминиро-ванной системы на основе методов вариации-онного исчисления.
- •Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Управление ресурсами и задача линейного программирования. Примеры, геометрическая интерпретация.
- •Решение задачи линейного программиро-вания на основе симплекс – метода.
- •Теорема о нормальной корреляции и ее следствия.
- •Решение задачи линейного программиро-вания на основе симплекс – метода
- •2.Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Синтез структуры сложной системы управления. Метод ветвей и границ.
- •Принципы координации в задачах управления сложными объектами.
- •2. Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Метод анализа иерархий.
- •2. Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Общее решение задачи автоматического управления без ограничений для детерминированной системы на основе методов вариационного исчисления.
- •2. Оптимальное управление в стохастических системах. Принцип разделения в непрерывных стохастических системах.
- •Принципы координации в задачах управления сложными объектами.
- •2. Уравнения фильтра Калмана в дискретном времени. Пример постановки задачи стохастического управления (управление нефтехранилищем).
- •Синтез структуры сложной системы управления. Метод ветвей и границ.
- •2. Принцип максимума Понтрягина и решение задачи о быстродействии при переводе материальной точки в начало координат.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Решение задачи о пошаговом распределении ресурсов на основе принципа оптимальности Беллмана.
- •Принцип максимума Понтрягина и решение задачи о быстродействии (задача о «лифте»).
- •2. Применение микропроцессоров и микро – эвм в цифровых системах управления.
Общая постановка задачи оптимальной фильтрации и методика ее решения.
Для решения линейно-квадратичной задачи управления требуется найти оценку текущего состояния объекта управления, обладающую рядом свойств:
рекуррентность алгоритма получения оценки;
ортогональность ошибки оценки и самой оценки;
оптимальность в смысле минимума дисперсии ошибки.
Решение
подобной задачи осуществляется методами
теории оптимальной фильтрации. Общая
постановка задачи в дискретном времени.
Пусть
заданы два уравнения: состояний и
наблюдений
 ,
,
 ,
,
 ,
,
 .
Требуется
по полученной совокупности наблюдений
.
Требуется
по полученной совокупности наблюдений
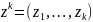 за k
шагов получить апостериорную
оптимальную в среднеквадратичном
оценку
за k
шагов получить апостериорную
оптимальную в среднеквадратичном
оценку
 путем вычисления апостериорной плотности
путем вычисления апостериорной плотности
 .
.
Такая
оценка является экстраполяцией состояния
объекта на один шаг вперед. Иногда
рассматри-вают оценку
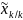 (оценка вида «точка в точке»), основой
получения которой является апостери-орная
плотность распределения
(оценка вида «точка в точке»), основой
получения которой является апостери-орная
плотность распределения
 .
В качестве показателя
оптимальности
некоторой используемой оценки
.
В качестве показателя
оптимальности
некоторой используемой оценки
 рассматривается
рассматривается

 ]
] ,
где N
- симметричная, положительно определенная
матрица. Если
,
где N
- симметричная, положительно определенная
матрица. Если
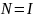 ,
то
,
то
 .
Оценка
называется оптимальной в среднеквадратичном,
если она обеспечивает минимизацию
величины
.
Оценка
называется оптимальной в среднеквадратичном,
если она обеспечивает минимизацию
величины .
Дифференцируя
внутренний интеграл
.
Дифференцируя
внутренний интеграл
 по компонентам
,
получим необходимое условие минимума
по компонентам
,
получим необходимое условие минимума
 =0.
Отсюда
=0.
Отсюда
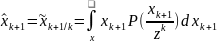 .
Оптимальная
оценка в среднеквадратичном есть
апостериорное математическое ожидание
вектора
относительно полученных наблюдений
.
Оптимальная
оценка в среднеквадратичном есть
апостериорное математическое ожидание
вектора
относительно полученных наблюдений
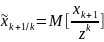 .
Общая
методика нахождения апостериорной
плотности распределения вероятностей.
Пусть
на некотором шаге известна плотность
.
Общая
методика нахождения апостериорной
плотности распределения вероятностей.
Пусть
на некотором шаге известна плотность
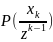 .
Тогда в соответствии с формулой Байеса
плотность
.
Тогда в соответствии с формулой Байеса
плотность
 на следующем шаге имеет вид
на следующем шаге имеет вид
 ,
,

 .
Учтем, что
при известном
для используемых моделей состо-яний и
наблюдений
.
Учтем, что
при известном
для используемых моделей состо-яний и
наблюдений
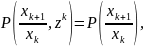
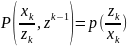 .
Это означает
марковский
характер
эволюции процесса
.
Это означает
марковский
характер
эволюции процесса
 и совместно марковский характер
процессов
и совместно марковский характер
процессов
 .
Если известна
начальная плотность
.
Если известна
начальная плотность
 ,
приведенные уравнения позволяют
получить рекуррентное выражение для
апостериорной плотности текущего
состояния
и, соответ-ственно, оптимальную оценку
.
Постановка задачи оптимальной линейной
фильтрации. Пусть
,
приведенные уравнения позволяют
получить рекуррентное выражение для
апостериорной плотности текущего
состояния
и, соответ-ственно, оптимальную оценку
.
Постановка задачи оптимальной линейной
фильтрации. Пусть

 Пусть
законы распределения шумов
Пусть
законы распределения шумов
 ,
а также начального вектора
являются гауссовскими
,
а также начального вектора
являются гауссовскими

 ,
,
 – независимые в дискретном времени,
друг относительно друга и
величины.Требуется
найти оптимальную в среднеквадратичном
оценку в задаче линейной фильтрации
(фильтр Калмана-Бьюси в дискретном
времени). Плотность
при высказанных предположениях имеет
гауссовский вид
– независимые в дискретном времени,
друг относительно друга и
величины.Требуется
найти оптимальную в среднеквадратичном
оценку в задаче линейной фильтрации
(фильтр Калмана-Бьюси в дискретном
времени). Плотность
при высказанных предположениях имеет
гауссовский вид
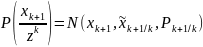 ,
,
 – матрица ковариации ошибки
– матрица ковариации ошибки
 – отклонения
от условного среднего
.
Действительно, каждый вектор
есть сумма двух гауссовских величин
– отклонения
от условного среднего
.
Действительно, каждый вектор
есть сумма двух гауссовских величин
 и
.
Поэтому плотность распределения
совокупности
и
.
Поэтому плотность распределения
совокупности
 является совместно гауссовской. В
теории вероятностей показано, что в
этом случае образу-ющие ее условные
плотности распределения вероятностей
является совместно гауссовской. В
теории вероятностей показано, что в
этом случае образу-ющие ее условные
плотности распределения вероятностей
 также являются гауссовскими.
также являются гауссовскими.
Контрольно-измерительный материал № 3
