- •Определение систем в рамках теоретико - множественного подхода. Математические модели простых динамических систем.
- •Принцип разделения в цифровых системах управления. Обоснование для линейно – квадратичной задачи управления в дискретном времени.
- •Решение задачи линейного программиро-вания на основе симплекс- метода.
- •Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Теорема о нормальной корреляции и ее следствия.
- •Классификация систем управления. Основ-ные этапы синтеза сложных систем управления.
- •Метод анализа иерархий.
- •Устойчивость динамических систем. Теорема Ляпунова в непрерывном и дискретном времени.
- •Иерархическая схема управления сложным объектом. Основные принципы иерархического управления.
- •Управляемость и наблюдаемость систем управления.
- •Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Постановка и пример задачи автоматичес-кого управления для непрерывных динамичес-ких систем. Задачи Больца, Лагранжа, Майера.
- •Метод анализа иерархий.
- •Общее решение задачи автоматического управления без ограничений для детерминиро-ванной системы на основе методов вариации-онного исчисления.
- •Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Управление ресурсами и задача линейного программирования. Примеры, геометрическая интерпретация.
- •Решение задачи линейного программиро-вания на основе симплекс – метода.
- •Теорема о нормальной корреляции и ее следствия.
- •Решение задачи линейного программиро-вания на основе симплекс – метода
- •2.Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Синтез структуры сложной системы управления. Метод ветвей и границ.
- •Принципы координации в задачах управления сложными объектами.
- •2. Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Метод анализа иерархий.
- •2. Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Общее решение задачи автоматического управления без ограничений для детерминированной системы на основе методов вариационного исчисления.
- •2. Оптимальное управление в стохастических системах. Принцип разделения в непрерывных стохастических системах.
- •Принципы координации в задачах управления сложными объектами.
- •2. Уравнения фильтра Калмана в дискретном времени. Пример постановки задачи стохастического управления (управление нефтехранилищем).
- •Синтез структуры сложной системы управления. Метод ветвей и границ.
- •2. Принцип максимума Понтрягина и решение задачи о быстродействии при переводе материальной точки в начало координат.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Решение задачи о пошаговом распределении ресурсов на основе принципа оптимальности Беллмана.
- •Принцип максимума Понтрягина и решение задачи о быстродействии (задача о «лифте»).
- •2. Применение микропроцессоров и микро – эвм в цифровых системах управления.
Линейный регулятор. Пример решения задачи лк – управления.
![]()
Схема
управления на основе П-регулятора
(про-порциональный регулятор).
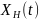 – желаемая траектория изменения
параметров объекта, которая называется
траекторией «невозмущенного» дви-жения
или задающим воздействием;
– желаемая траектория изменения
параметров объекта, которая называется
траекторией «невозмущенного» дви-жения
или задающим воздействием;
 –
фак-тическая траектория, отличающаяся
от желаемой в силу наличия неопределенностей
и возмущений ξ;
–
фак-тическая траектория, отличающаяся
от желаемой в силу наличия неопределенностей
и возмущений ξ;
 – отклонение
невозмущенного и возмущенного движений;
– отклонение
невозмущенного и возмущенного движений;
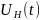 –
программное управление, определенное
заранее для идеальных условий формирования
–
программное управление, определенное
заранее для идеальных условий формирования
 ;
;
 –
управляющее воздействие, реально
прикладываемое к объекту;
–
управляющее воздействие, реально
прикладываемое к объекту;
 – коррекция
программного управления, связанная с
отклонением x(t)
от желаемой траектории линейной обратной
связью. Минимизация
квадрата отклонения
и квадрата
коррекции программ-много управления
– коррекция
программного управления, связанная с
отклонением x(t)
от желаемой траектории линейной обратной
связью. Минимизация
квадрата отклонения
и квадрата
коррекции программ-много управления
 обеспечивает минимизацию дисперсии
ошибки при форми-ровании управляющих
параметров объектов и энергетических
затрат на управление. Замкнутая
П-регулятором система для процессов
обеспечивает минимизацию дисперсии
ошибки при форми-ровании управляющих
параметров объектов и энергетических
затрат на управление. Замкнутая
П-регулятором система для процессов
 ,
описывающих отклонения от
,
,
описывающих отклонения от
,
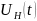 ,
понимаемых теперь как состояние и
управление имеет вид
,
понимаемых теперь как состояние и
управление имеет вид
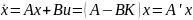 .
Ос-новным требованием к выбору
П-регулятора яв-ляется его устойчивость.
Как следует из приведен-ного соотношения,
устойчивость системы опреде-ляется
свойствами собственных чисел матрицы
.
Ос-новным требованием к выбору
П-регулятора яв-ляется его устойчивость.
Как следует из приведен-ного соотношения,
устойчивость системы опреде-ляется
свойствами собственных чисел матрицы
 .
Во многих случаях стабилизировать
объекты с помощью П-регулятора не
удается и используют другие виды
регуляторов. Для их описания имеется
следующие обобщенные блок-схемы.
.
Во многих случаях стабилизировать
объекты с помощью П-регулятора не
удается и используют другие виды
регуляторов. Для их описания имеется
следующие обобщенные блок-схемы.
![]()
 .
При описании регуляторов в этом случае
удобно частотное представление процесса
( б), основанное на использовании
преобразования Лапласа. Для исходной
временной функции оригинала
.
При описании регуляторов в этом случае
удобно частотное представление процесса
( б), основанное на использовании
преобразования Лапласа. Для исходной
временной функции оригинала
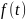 ее изображение по Лапласу
ее изображение по Лапласу
 имеет вид
имеет вид
 которое определено для функций, растущих
не быстрее экспоненты
которое определено для функций, растущих
не быстрее экспоненты
 .
Передаточной функцией цепи называется
отношение
.
Передаточной функцией цепи называется
отношение

 -
изображение входной временной функции
-
изображение входной временной функции
 ;
;
 – изображение выходной временной
функции
– изображение выходной временной
функции
 .
Соответственно на (б)
.
Соответственно на (б)
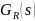 – передаточная функция регулятора, а
– передаточная функция регулятора, а
 – объек-та управления. Передаточная
функция замкнутой системы от
– объек-та управления. Передаточная
функция замкнутой системы от
 имеет вид
имеет вид
 ,
,
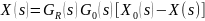 .
.
Пропорциональные П-регуляторы:

Пропорционально-дифференциальные
ПД-регуляторы :
 ,
,
 ;
;
Пропорционально-интегральные ПИ-регуляторы:
 Пропорционально-интегродифференциальные
ПИД-регуляторы :
Пропорционально-интегродифференциальные
ПИД-регуляторы :

 .
.
Пример – задача линейного П-регулирования процесса намотки провода.
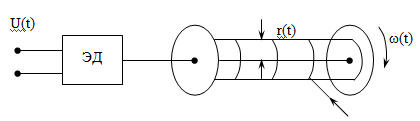
Скорость
намотки должна быть постоянной
 .
Увеличение
радиуса
.
Увеличение
радиуса
 требует уменьшать угловую скорость
требует уменьшать угловую скорость
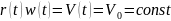 .
Увеличение
радиуса
приводит к
увеличению момента инерции
.
Увеличение
радиуса
приводит к
увеличению момента инерции
 .
Уравнение движения катушки при этом
имеет вид
.
Уравнение движения катушки при этом
имеет вид
 ,
,
 – напряжение на входе электродвига-теля;
– напряжение на входе электродвига-теля;
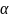 –
коэффициент пропорциональности между
вращающим моментом двигателя и входным
напряжением;
–
коэффициент пропорциональности между
вращающим моментом двигателя и входным
напряжением;
 – коэффициент трения. Управле-нием
является
,
регулируемой величиной –
– коэффициент трения. Управле-нием
является
,
регулируемой величиной –
 ,
которую необходимо менять, чтобы
выполнялось
,
которую необходимо менять, чтобы
выполнялось
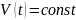 .
За время
.
За время
 обмотки одного ряда радиус изменяется
от
обмотки одного ряда радиус изменяется
от
 до
до

 – некоторый
коэффициент, характеризующий провод.
При
– некоторый
коэффициент, характеризующий провод.
При
 можно записать, что
можно записать, что
 .
Для круга радиуса r
момент инерции пропорционален
.
Для круга радиуса r
момент инерции пропорционален

 ,
,
 – известные
функции. Желаемое значение угловой
скорости определяется как функция
времени в виде
– известные
функции. Желаемое значение угловой
скорости определяется как функция
времени в виде
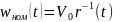 ,
а номинальное
управляющее напряжение в виде
,
а номинальное
управляющее напряжение в виде
 .Для
отклонений возмущенных в реальности
траекторий соответствующих переменных
от невозмущенных можно записать
.Для
отклонений возмущенных в реальности
траекторий соответствующих переменных
от невозмущенных можно записать
 ,
,
 .
Окончательно
получаем уравнение линейного вида
.
Окончательно
получаем уравнение линейного вида



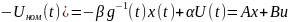
Критерий качества, подлежащий минимизации в данном случае, естественно выбрать в виде
 ,
,
 ,
,
первое
слагаемое пропорционально кинетической
энергии вращающейся катушки; второе
слагаемое пропорционально энергии,
расходуемой электродвигателем.Получили
линейно-квадратичную задачу управления,
в которой решение имеет вид
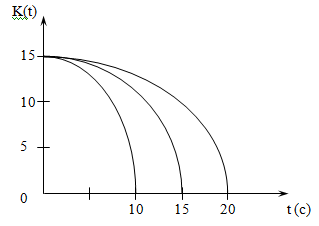
 P(t)–
есть решение уравнения Риккати
P(t)–
есть решение уравнения Риккати
 ,
P(T)=0. Это
уравнение можно численно проинтегрировать
и получить конкретные зависимости для
оптимального коэффициента линейной
обратной связиK(T).
,
P(T)=0. Это
уравнение можно численно проинтегрировать
и получить конкретные зависимости для
оптимального коэффициента линейной
обратной связиK(T).