
- •Определение систем в рамках теоретико - множественного подхода. Математические модели простых динамических систем.
- •Принцип разделения в цифровых системах управления. Обоснование для линейно – квадратичной задачи управления в дискретном времени.
- •Решение задачи линейного программиро-вания на основе симплекс- метода.
- •Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Теорема о нормальной корреляции и ее следствия.
- •Классификация систем управления. Основ-ные этапы синтеза сложных систем управления.
- •Метод анализа иерархий.
- •Устойчивость динамических систем. Теорема Ляпунова в непрерывном и дискретном времени.
- •Иерархическая схема управления сложным объектом. Основные принципы иерархического управления.
- •Управляемость и наблюдаемость систем управления.
- •Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Постановка и пример задачи автоматичес-кого управления для непрерывных динамичес-ких систем. Задачи Больца, Лагранжа, Майера.
- •Метод анализа иерархий.
- •Общее решение задачи автоматического управления без ограничений для детерминиро-ванной системы на основе методов вариации-онного исчисления.
- •Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Управление ресурсами и задача линейного программирования. Примеры, геометрическая интерпретация.
- •Решение задачи линейного программиро-вания на основе симплекс – метода.
- •Теорема о нормальной корреляции и ее следствия.
- •Решение задачи линейного программиро-вания на основе симплекс – метода
- •2.Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Синтез структуры сложной системы управления. Метод ветвей и границ.
- •Принципы координации в задачах управления сложными объектами.
- •2. Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Метод анализа иерархий.
- •2. Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Общее решение задачи автоматического управления без ограничений для детерминированной системы на основе методов вариационного исчисления.
- •2. Оптимальное управление в стохастических системах. Принцип разделения в непрерывных стохастических системах.
- •Принципы координации в задачах управления сложными объектами.
- •2. Уравнения фильтра Калмана в дискретном времени. Пример постановки задачи стохастического управления (управление нефтехранилищем).
- •Синтез структуры сложной системы управления. Метод ветвей и границ.
- •2. Принцип максимума Понтрягина и решение задачи о быстродействии при переводе материальной точки в начало координат.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Решение задачи о пошаговом распределении ресурсов на основе принципа оптимальности Беллмана.
- •Принцип максимума Понтрягина и решение задачи о быстродействии (задача о «лифте»).
- •2. Применение микропроцессоров и микро – эвм в цифровых системах управления.
Общее решение задачи автоматического управления без ограничений для детерминиро-ванной системы на основе методов вариации-онного исчисления.
Общее
решение задачи оптимального управления
со свободным правым концом для
детерминиро-ванной системы
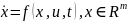 ,
,
 без ограничений
на управление.
Отсутствие ограничений на управление
означает, что его возможные значения
без ограничений
на управление.
Отсутствие ограничений на управление
означает, что его возможные значения
 ,
где
,
где
 – множество ограниченных непрерывных
функций. Такая
задача может быть решена в рамках
методов вариационного исчисления.
Вариа-ционное
исчисление изучает методы нахождения
экстремума функционалов. Вариацией
функции y(x)
есть функция от X
вида
– множество ограниченных непрерывных
функций. Такая
задача может быть решена в рамках
методов вариационного исчисления.
Вариа-ционное
исчисление изучает методы нахождения
экстремума функционалов. Вариацией
функции y(x)
есть функция от X
вида
 ,
определяемая как разность новой функции
Y(x)
иy(x).
Пусть дана функция
,
определяемая как разность новой функции
Y(x)
иy(x).
Пусть дана функция
 .
Если она имеет непрерывные частные
производ-ные второго порядка, то ее
приращение, вызванное вариациями
.
Если она имеет непрерывные частные
производ-ные второго порядка, то ее
приращение, вызванное вариациями
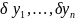 ,
определяется как
,
определяется как
 ,
,
 .
В приведенном выражении (формуле
Тейлора) первый и второй член – есть
первая
.
В приведенном выражении (формуле
Тейлора) первый и второй член – есть
первая
 и вторая
и вторая
 вариации функцииF.
В дальнейшем будем использовать
следующие обозначения. Для скалярной
функции
вариации функцииF.
В дальнейшем будем использовать
следующие обозначения. Для скалярной
функции
 векторного аргумента
векторного аргумента
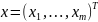
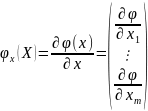 .
.


Решение
поставленной задачи нахождения минимума
функционала J
осуществляется по следующей
схеме.Образуется вспомогательный
функционал
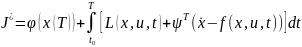 ,
где
,
где
 – вектор множителей Лагранжа.
Необходимость
введения вспомогательного функционала
определяется необходимостью учета
характера движения. Вводится
скалярная функция, называемая
гамильтонианом
– вектор множителей Лагранжа.
Необходимость
введения вспомогательного функционала
определяется необходимостью учета
характера движения. Вводится
скалярная функция, называемая
гамильтонианом
 .
Интегрируя по частям последнее слагаемое
в правой части, получим
.
Интегрируя по частям последнее слагаемое
в правой части, получим

 .Найдем
теперь вариацию функционала
.Найдем
теперь вариацию функционала
 ,
соответствующую вариациям управления
u(t)
с учетом возникающих при этом вариаций
x(t)
,
соответствующую вариациям управления
u(t)
с учетом возникающих при этом вариаций
x(t)

 .Для
того, чтобы исключить влияние вариаций
.Для
того, чтобы исключить влияние вариаций
 ,
вызванных вариациями по управлению
,
вызванных вариациями по управлению
 ,
на вариации функционала
,
на вариации функционала
 ,
выберем множители
,
выберем множители
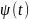 таким образом, чтобы коэффициенты при
,
таким образом, чтобы коэффициенты при
,
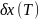 обратились в ноль
обратились в ноль
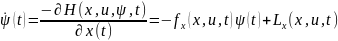 ;
;
 .
Эта система уравнений называется
сопряженной системой. При
выборе ψ(t)
в соответствии с сопряженной системой
уравнение для
имеет вид
.
Эта система уравнений называется
сопряженной системой. При
выборе ψ(t)
в соответствии с сопряженной системой
уравнение для
имеет вид
 .
(1)
Это уравнение
определяет первую вариацию функционала
.
Поскольку J=
на траекториях решения уравнения,
описывающего поведение системы, то и
.
(1)
Это уравнение
определяет первую вариацию функционала
.
Поскольку J=
на траекториях решения уравнения,
описывающего поведение системы, то и
 .
Если J
достигает экстремума, то
.
Если J
достигает экстремума, то
 для произвольных
для произвольных
 .
.
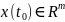 фиксировано,
тогда
фиксировано,
тогда
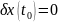 .
. – множество ограниченных непрерывных
функций, необходимое условие экстремума
имеет вид
– множество ограниченных непрерывных
функций, необходимое условие экстремума
имеет вид
 (2). Уравнения (1) и (2) это уравнения
Эйлера-Лагранжа. Они дают стационарное
решение – необходимое условие минимума
функционала потерь.
Достаточное
условие определяется
на основе определения еще и знака
второй вариации
(2). Уравнения (1) и (2) это уравнения
Эйлера-Лагранжа. Они дают стационарное
решение – необходимое условие минимума
функционала потерь.
Достаточное
условие определяется
на основе определения еще и знака
второй вариации
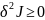 .Таким
образом, для того, чтобы найти
.Таким
образом, для того, чтобы найти
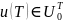 ,
нужно решить систему уравнений порядка
2m
следующего вида:
,
нужно решить систему уравнений порядка
2m
следующего вида:
 ,
,
 ,
где u(t)
определяется из условия
,
где u(t)
определяется из условия
 .Система
уравнений имеет m
краевых условий на левом конце и m
краевых условий на правом конце
.Система
уравнений имеет m
краевых условий на левом конце и m
краевых условий на правом конце
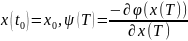 .Это
общее решение задачи в рамках классических
методов вариационного исчисления.
.Это
общее решение задачи в рамках классических
методов вариационного исчисления.
