Контрольно-измерительный материал № 1

1. Определение систем в рамках теоретико - множественного подхода. Математические модели простых динамических систем.

Система (С) – целостное, органично единое образование, состоящее из множества элементов, находящихся в отношениях или связях друг с другом.

Целостность – важнейшая характеристика С, которая проявляется в том, что в процессе взаимодействия элементов, входящих в состав системы, появляются принципиально новое качество, свойство, которым не обладает ни один из входящих в С элементов.

Структура – описание совокупности элементов (состав С) и наиболее устойчивых связей между ними.

Внешняя среда – совокупность элементов (объектов) естественного или искусственного происхождения, не входящих в состав системы, но оказывающих на нее определенное воздействие и определяющих существенные условия ее функционирования.

Системы делятся на простые и сложные:

1. по количеству входящих в нее элементов

2. по сложности выполняемых функций

3. по возможности формализованного описания системы

Сложная система – это объект, который можно описать не менее, чем на двух математических языках. Для простой системы характерна возможность корректного и законченного описания в рамках единого математического аппарата.

Иерархия – расположение частей и элементов целого в порядке от высшего к низшему.

Любая С определяется тремя основными категориями: элементы, отношения, свойства.

Модель (лат. «мера») – это объект-заменитель объекта-оригинала, обеспечивающий изучение наиболее существенных в интересующем нас аспекте свойств оригинала и, наоборот, позволяющий абстрагироваться от его несущественных в рамках данного рассмотрения свойств.

Модель функционирования С, обозначает модель, обеспечивающую предсказание изменения состояний системы во времени, то есть ориентированную на описание динамики ее функционирования

Где S – система, задаваемая в данном случае как n-арное отношение или подмножество декартова произведения множеств .

В условиях предельно нечеткого вербального описания систему можно представить в виде . Где A –множество лингвистических переменных терм, определяющих объекты, а B – множество функторов – лингвистических переменных, определяющих отношения (формы связи) между ними. При реализации функционального подхода С определяют как , где X – множество входных объектов, а Y – множество выходных объектов. В более характерном случае для определения системы в рамках функционального подхода используется понятие отображения или функции . Для любых ,xS . Определенная таким образом система называется функциональной.

Понятие временной системы. Вводится индексирующее множество T , а элементы входного и выходного множеств определяются как функции вида Т: . Систему называют временной системой.

1. Детерминированные модели в непрерывном времени. 0бщий вид модели детерминированной системы, описываемой обыкновенным дифференциальным уравнением:

,…

, где - вектор состояния системы; — вектор возмущающих или управляющих внешних воздействий, зависимость которого от времени носит детерминированный характер; f(...) — заданная вещественная непрерывная и дифференцируемая вектор-функция своих аргументов. Общий вид решения уравнения:

2. Детерминированные модели в дискретном времени. . Для описания такого поведения используют уравнения в конечных разностях.. Общий вид таких уравнений:

— значения соответствующих векторных величин в дискретные моменты времени; f(...)— вещественная непрерывная функция своих аргументов известного вида. Детерминированная линейная система описывается линейными разностными уравнениями вида

где — матрицы соответствующей размерности.

3. Стохастические модели в непрерывном времени. Стохастические дифференциальные уравнения вида

матричная функция известного вида размера , определяющая добавление стохастической составляющей; мерный случайный процесс типа белого шума с нулевым математическим ожиданием и ковариационной матрицей вида 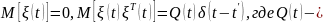матричная функция размера . , где C(t) - матричная функция размера .

4. Стохастические модели в дискретном времени. Формализованное описание системы в этой ситуации определяется разностными уравнениями вида

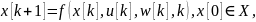
независимая в дискретном времени центрированная гауссовская случайная последовательность