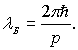19. Релятивистский импульс. Закон взаимосвязи массы и энергии

В теории относительности импульс определяется по формуле

Величину называют релятивистской массой, измеренной и ИСО, относительно которой движется тело со скоростью u

Следовательно, .

При υ=c получим, что m0=m.0. Это уравнение имеет единственное решение:m0=0. Т.е. со скоростью, равной скорости света может двигаться только тело, имеющее массу покоя, равную нулю. Это говорит о предельном характере скорости света для материальных тел.

Полную энергию свободного тела можно определить как произведение его релятивистской массы на квадрат скорости света в вакууме:

Полная энергия тела пропорциональна его массе. В той ИСО, где тело покоится, его собственная энергия (энергия покоя или внутренняя энергия) равна: .Энергия покоя тела является его внутренней энергий. Она состоит из суммы энергий покоя всех частиц тела, кинетической энергии всех частиц относительно общего центра масс и потенциальной энергии их взаимодействия. Следовательно, энергия покоя (и масса покоя) тела не равна сумме энергий покоя (масс покоя) частиц, из которых состоит тело. Т.е. в релятивистской механике не выполняется закон сохранения массы покоя. Например, масса покоя атомного ядра меньше суммы масс покоя частиц, входящих в ядро.

Кинетическая энергия свободного тела представляет собой разность между полной энергией тела и энергией покоя: .

Т.о. при малых скоростях получаем известную формулу .

В этом случае кинетическая энергия значительно меньше энергии покоя. В случае релятивистских частиц - наоборот, можно считать, что полная энергия частицы равна кинетической энергии.

20. Уравнение свободных гармонических электромагнитных колебаний. Колебательный контур. Энергия колебаний. Параметры затухающих колебаний

Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддерживания электромагнитных колебаний используется колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.

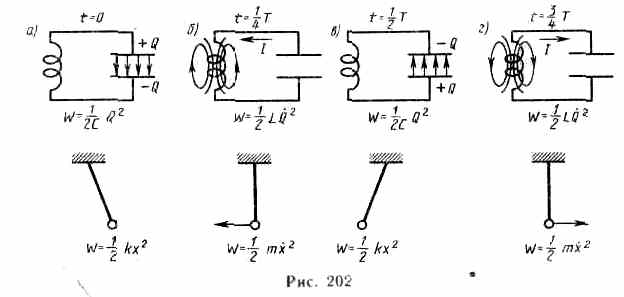
Рассмотрим последовательные стадии колебательного процесса в идеализированном контуре, сопротивление которого пренебрежимо мало (R0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Тогда в начальный момент времени t=0 (рис. 202, а) между обкладками конденсатора возникнет электрическое поле, энергия которого

(¹/₂C)Q² Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (она равна ¹/₂LQ² ) —возрастать.

Так как R0, то, согласно закону сохранения энергии, полная энергия

так как она на нагревание не расходуется. Поэтому в момент t=¹/₄ Т, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения

(рис. 202, б). Начиная с этого момента ток в контуре будет убывать; следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцируется ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который в конце концов обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 202, в). Далее те же процессы начнут протекать в обратном направлении (рис. 202, г) и система к моменту времени t=T придет в первоначальное состояние (рис. 202, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т. е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, при чем колебания сопровождаются превращениями энергий электрического и магнитного полей.

Электрические колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рис.202 внизу), сопровождающимися взаимными превращениями потенциальной и кинетической энергий маятника. В данном случае энергия электрического поля конденсатора (Q²/(2C)) аналогична потенциальной энергии упругой деформации (kx²/2), энергия магнитного поля катушки (LQ²/2) — кинетической энергии (mx²/2), сила тока в контуре — скорости движения маятника. Индуктивность L играет роль массы т, а сопротивление контура — роль силы трения, действующей на маятник.

Согласно закону Ома, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R,

ir+u_c=ξ_s,

где IR — напряжение на резисторе, U_C=Q/C— напряжение на конденсаторе, ξ_s=-LdI/dt — э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока (ξ_s, —единственная э.д.с. в контуре).. Следовательно,

Разделив на L и подставив I=Q и dI/dt=Q, получим дифференциальное уравнение колебаний заряда Q в контуре:

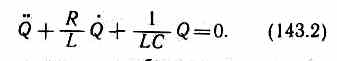
В данном колебательном контуре внешние э.д.с. отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре:

Из выражений вытекает, что заряд Q совершает гармонические колебания по закону

Q = Q_mcos(₀t+),

где Q_m — амплитуда колебаний заряда конденсатора с циклической частотой ₀, называемой собственной частотой контура, т. е.

₀=1/LC,

и периодом

T=2LC.

Формула впервые была получена У. Томсоном и называется формулой Томсона.

Отметим в заключение, что при увеличении коэффициента затухания δ период затухающих колебании увеличивается и при δ=ω0 равен бесконечности, т. е. движение перестает быть периодическим. В этом случае колеблющаяся величина асимптотически стремится к нулю, когда t→∞. Данный процесс не будет колебательным. Он называется апериодическим.

Затухание свободных колебаний

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением: (7.1.1)

где - коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Например, для пружинного маятника где r - коэффициент сопротивления, т.е. коэффициент пропорциональности между скоростью и силой сопротивления. Для затухающих колебаний в колебательном контуре : , где R - величина активного сопротивления контура.

Для решения уравнения производится подстановка . Эта подстановка приводит к характеристическому уравнению: которое имеет два корня: При не слишком большом затухании подкоренное выражение будет отрицательным. Если его представить в виде , где w - вещественная положительная величина, называемая циклической частотой затухающих колебаний и равная , то корни уравнения запишутся в виде: и

Общим решением уравнения будет функция:

которую можно представить в виде:

Период затухающих колебаний определяется формулой:

При незначительном затухании период колебаний практически равен . С ростом период увеличивается. Из соотношения следует, что . Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:

Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз.

22. Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.

Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.

Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно: Δl = x – y = x – ym cos ωt.

Второй закон Ньютона для тела массой m принимает вид : ma = –k(x – y) = –kx + kym cos ωt.

В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.

Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой (рис. 2.5.2).

При резонансе амплитуда xm колебания груза может во много раз превосходить амплитуду ym колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.

Ток, изменяющийся во времени по значению и направлению, называется переменным. В практике применяют периодически изменяющийся по синусоидальному закону переменный ток

Синусоидальные величины характеризуются следующими основными параметрами: периодом, частотой, амплитудой, начальной фазой или сдвигом фаз.

Период (T) - время (с), в течение которого переменная величина совершает полное колебание.

Частота - число периодов в секунду. Единица измерения частоты - Герц (сокращенно Гц), 1 Гц равен одному колебанию в секунду. Период и частота связаны зависимостью

T = 1 / f

Изменяясь с течением времени, синусоидальная величина (напряжение, ток, ЭДС) принимает различные значения. Значение величины в данный момент времени называют мгновенным.

Амплитуда - наибольшее значение синусоидальной величины. Амплитуды тока, напряжения и ЭДС обозначают прописными буквами с индексом: Im, Um, Em, а их мгновенные значения - строчными буквами i, u, e.

Мгновенное значение синусоидальной величины, например тока, определяют по формуле

i = Imsin(ωt + ψ), где ωt + ψ — фаза-угол, определяющий значение синусоидальной величины в данный момент времени; ψ - начальная фаза, т. е. угол, определяющий значение величины в начальный момент времени.

Синусоидальные величины, имеющие одинаковую частоту, но разные начальные фазы, называются сдвинутыми по фазе.

Разница начальных фаз φ = ψi − ψu определяет угол сдвига фаз. На рис. 2 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны ψi = ψu, то разница ψi − ψu = 0 и, значит, сдвига фаз нет φ = 0 (рис. 3).

Эффективность механического и теплового действия переменного тока оценивается действующим его значением. Действующее значение переменного тока равно такому значению постоянного тока, который за время, равное одному периоду переменного тока, выделит в том же сопротивлении такое же количество тепла, что и переменный ток.

23. Нетрудно написать уравнение сферической волны. Положение колеблющейся частицы определяется в этом случае только ее расстоянием от источника колебаний r, т.е. фаза колебаний должна иметь вид ωt – kr + a. Амплитуда колебаний в сферической волне, однако, не будет оставаться постоянной — она убывает с расстоянием, как 1/r. Последнее утверждение вытекает из требования, чтобы поток энергии, переносимый волной через поверхность сферы любого, сколь угодно большого, радиуса оставался постоянным. Таким образом, сферическая волна должна иметь следующий вид: u(r,t) = cos(ωt – kr + a), где a— постоянная величина, численно равная амплитуде

Найдем уравнение плоской волны, бегущей в трехмерном пространстве вдоль произвольного направления n. Выберем систему координат и возьмем волновую поверхность волны, находящуюся на расстоянии l от начала координат (рис.). Это будет плоскость, перпендикулярная вектору n. Если волна в начале координат задана уравнение

u(0,t) = u0×cos(ωt + a), то колебания частиц на выбранной волновой поверхности будут иметь вид: u(0,t) = u0×cos(ωt –kl + a). Написанному выше уравнению можно придать вид: u(,t) = u0×cos(ωt - k× + a).

Введем вектор

равный по величине волновому числу и направленный вдоль вектора n направления распространения волны. Величина называется волновым вектором. С его помощью уравнение плоской бегущей волны, распространяющейся в произвольном направлении n, приобретает вид: u( ,t)= u0cos(ωt – + a)

Продифференцируем выражение по каждой из этих переменных дважды, пользуясь тем, что = kx+ ky+ kz

Складывая производные по координатам и выражая правую часть полученного выражения через производную по времени, находим:

Наконец, заменяя ω/k на фазовую скорость волны, окончательно получаем:

Это и есть общий вид волнового уравнения.

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной. Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной.Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн. Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты. Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой. Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок

В этой модели инертные и упругие свойства разделены. Шарики обладают массой m, а пружинки – жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия (см. §1.12). В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.

Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных. Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна. В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появляется. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.

24. Рассмотрим несколько характерных случаев:

1. Ортогональность поляризаций волн. При этом и . Интерференционные полосы отсутствуют, а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы.

2. В случае равенства частот волн и контраст полос не зависит от времени экспозиции .

3. В случае значение функции и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0

4. В случае контраст полос существенным образом зависит от разности частот и времени экспозиции.

Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.

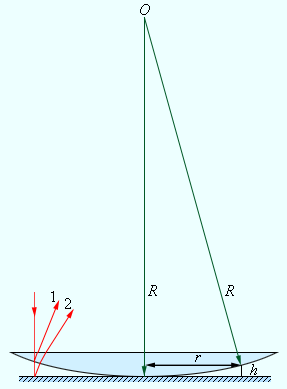
Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона

Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1 и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.

Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при , где — длина волны. Если нм, то толщина плёнки равняется 550:4=137,5 нм.

Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей

— условие максимума;

— условие минимума,

где k=0,1,2... и — оптическая длина пути первого и второго луча, соответственно.

Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.

ФРЕНЕЛЯ ЗЕРКАЛА (бизеркала Френеля) - оптическое устройство, предложенное в 1816 О. Ж. Френелем для наблюдения явления интерференции света. Ф. з. состоят из двух плоских зеркал I и II (рис.), образующих друг с другом угол, немного меньший 180°. Источник света S, отражённый в них, образует два близко расположенных мнимых изображения S1 и S2- Пучки света от этих изображений (когерентные, т. к. образованы одним источником) пересекаются под малым углом и дают интер-ференц. картину на экране АВ. Ф. з. используются в интерферометрии.

1. Существуют специальные приборы — интерферометры, действие которых основано на явлении интерференции. Их назначение — точное измерение длин волн, показателей преломления, коэффициентов линейного расширения и др. Действие всех интерферометров основано на одном и том же принципе, и интерферометры различаются лишь конструктивно. На рисунке представлена упрощенная схема интерферометра Майкельсона.

Монохроматический пучок света от источника S падает под углом 45° на плоскопараллельную пластинку Р1. Сторона пластинки, удаленная от S, покрыта тонким слоем серебра с таким расчетом, что он половину светового пучка пропустит, а половину отразит (полупрозрачная пластинка), т.е. здесь луч разделяется на две части: луч 1 отражается от посеребренного слоя, луч 2 проходит через него. Луч 1 отражается от зеркала М1 и, возвращаясь обратно, вновь проходит через пластинку P1 (луч 1'). Луч 2 идет к зеркалу М2, отражается от него, возвращается обратно и отражается от пластинки P1 (луч 2'). Так как первый луч проходит пластинку Р1 дважды, то для компенсации возникшей разности хода на пути второго луча ставится пластинка Р2 (точно такая же, как и P1 только не покрытая слоем серебра). Лучи 1' и 2' когерентны, следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала M1 и луча 2 от точки О до зеркала М2. При перемещении одного из зеркал на расстояние разность хода обоих лучей изменится на и в интерференционной картине максимум сдвинется на место минимума, и наоборот, т.е. интерференционный максимум сдвинется на половину расстояния между полосами. Такой сдвиг полос наблюдатель отчетливо увидит. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр для достаточно точных (-10-9 м) измерений длин (длины тел, длины световой волны, определений температурного коэффициента линейного расширения и др.).

2. Используя явление интерференции, можно оценить качество обработки поверхности изделия с точностью до 10-6 см. Для этого нужно создать тонкую клиновидную прослойку воздуха между поверхностью образца и очень гладкой эталонной пластинкой. Неровности поверхности вызовут заметные искривления интерференционных полос, образующихся при отражении света от проверяемой поверхности и нижней границы эталонной пластинки. На рисунке приведены наблюдаемые интерференционные картины при отступлении от требуемой точности обработки и при достижении необходимой точности обработки плоской поверхности детали .

3. Просветление оптики. Отполированная поверхность стекла отражает около 4% перпендикулярно падающего на нее света. Современные оптические приборы состоят из большого числа оптических стекол — линз, призм и т.д. Поэтому общие потери света в объективе фотоаппарата составляют около 25%, в микроскопе — 50% и т.д. В результате освещенность изображения получается малой, ухудшается также качество изображения.

25. Дифракционная решётка - оптический прибор, предназначенный для анализа спектрального состава оптического излучения. Дифракционная решётка состоит из тысяч узких и близко расположенных щелей. Из-за интерференции интенсивность света прошедшего через дифракционную решётку различна в различных направлениях. Имеются выделенные направления в которых световые волны от различных щелей решётки складываются в фазе, многократно усиливая друг друга. При освещении решётки монохроматическим светом на её выходе наблюдаются узкие лучи с большой интенсивностью. Так как направления на интерференционные максимумы зависят от длины волны, белый свет , прошедший через дифракционную решётку, будет расщепляться на множество лучей разного цвета. Таким образом мы можем исследовать спектральный состав света. Выражение для интерференционных максимумов одинаково для пары щелей и дифракционной решётки, но в последнем случае максимум оказывается намного более острым и интенсивным, обеспечивая высокое разрешение в спектроскопических исследованиях. Интенсивность максимумов также оказывается пропорциональной второй степени количества освещаемых щелей (штрихов).

Рассмотрим вначале две щели, на которые нормально падает плоская монохроматическая волна. Говоря о дифракции Фраунгофера, мы подразумеваем случай, когда наблюдение дифракционной картины производится на достаточно большом расстоянии от экрана с щелями. Количественный критерий дифракции Фраунгофера описывается следующей формулой: z >> d2/l, где z - расстояние от экрана с щелями до точки наблюдения. В непосредственной близости к щелям дифракционная картина будет описываться формулами Френеля.

Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка , что сильно упрощает теоретическое рассмотрение явления. Здесь — расстояние от отверстия или преграды до плоскости наблюдения, — длина волны излучения, а — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости)

Дифра́кция Френе́ля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

На рисунке схематично изображён (слева) непрозрачный экран с круглым отверстием (апертура), слева от которого расположен источник света. Изображение фиксируется на другом экране - справа. Вследствие дифракции свет, проходящий через отверстие, расходится, поэтому область, которая была затемнена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса. В точке наблюдения (занимаемое вторым экраном) волны или усиливают друг друга, или гасятся в зависимости от разности хода.

Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии - такая же, как при отсутствии экрана. Дифракция света, явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической оптики. Вследствие Д. с. при освещении непрозрачных экранов точечным источником света на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдается ряд светлых и тёмных дифракционных полос

Для нахождения результата интерференции вторичных волн Френель предложил метод разбиения волнового фронта на зоны, называемые зонами Френеля. 

Предположим, что источник светаточечный и монохроматический, а среда, в которой распространяется свет, изотропная. Волновой фронт в произвольный момент времени будет иметь форму сферы радиусом Каждая точка на этой сферической поверхности является вторичным источником волн. Колебания во всех точках волновой поверхности происходят с одинаковой часто-той и в одинаковой фазе. Следовательно, все эти вторичные источники когерентны. Для нахождения амплитуды колебаний в точке М необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности.

Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до точки М отличались на лямбда/2

26. дисперсия света – это зависимость показателя преломления вещества от частоты световой волны . Эта зависимость не линейная и не монотонная. Области значения ν, в которых (или ) соответствуют нормальной дисперсии света (с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров.

Дисперсия называется аномальной, если (или ),т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия.Зависимости n от ν и λ

В зависимости от характера дисперсии групповая скорость u в веществе может быть как больше, так и меньше фазовой скорости. Групповая скорость u связана с циклической частотой ω и волновым числом k соотношением: , где , . Тогда

Отсюда можно записать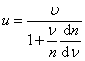

Таким образом, при нормальной дисперсии u < υ и .

При аномальной дисперсии u > υ, и, в частности, если , то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.

27.Поляризацияф света. Степень поляризации, получение поляризованного света. Закон Ампера.

ПОЛЯРИЗАЦИЯ СВЕТА - физ. характеристика оптич. излучения, описывающая поперечную анизотропию световых волн, т. е. неэквивалентность разл. направлений в плоскости, перпендикулярной световому лучу.

Степенью поляризации называется величина

 где I_max и I_min, - соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.

Существует несколько способов непосредственного получения поляризованного света. Эти способы основаны на использовании поляризованной флюоресценции, скользящего выхода лучей и пр. Когерентный поляризованный свет излучается лазерами. На практике такие методы применяются мало. Обычно для получения поляризованного света естественное излучение какого-либо источника пропускают через поляризатор. Действие поляризатора состоит в том, что он разделяет первоначальный пучок на две компоненты со взаимно перпендикулярными направлениями поляризации, пропускает одну компоненту и поглощает или отклоняет другую. Таким образом, теоретически пропускание поляризатора может составлять 50%. Практически пропускаемая компонента также частично поглощается материалом поляризатора, в результате чего пропускание несколько снижается. Осуществление процесса поляризации возможно за счет разных физических явлений: дихроизма, двойного лучепреломления отражения, рассеяния. Наиболее распространены дихроичные поляризаторы, но используются и двоякопреломляющие. Поляризаторы, основанные на отражении и рассеянии, применяют в исключительных случаях.

Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника. Что дает возможность применять этот закон для проводников различной формы.

28.Квантовая оптика. Законы теплового излучения, гипотеза Планка. Фотоны

КВАНТОВАЯ ОПТИКА - раздел оптики, изучающий микроструктуру световых полей и оптические явления в процессах взаимодействия света с веществом, в которых проявляется квантовая природа света.

Тепловое излучение представляет собой процесс распространения в пространстве внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются материальные частицы, входящие в состав вещества. Для распространения электромагнитных волн не требуется материальной среды, в вакууме они распространяются со скоростью света и характеризуются длиной волны λ или частотой колебаний ν

Закон Планка устанавливает зависимость спектральной интенсивности излучения абсолютно черного тела J_oλ от длины волны и температуры:

где λ — длина волны излучения, м; Т — температура излучающего тела, К;c₁=3,74·10^-16 Вт·м²; c₂=1,44·10^-2 м·К; e – основание натуральных логарифмов.

Закон Стефана — Больцмана. Плотность потока собственного интегрального излучения абсолютно черного тела можно найти на осно­вании закона Планка как суммарную энергию излучения тела по всем длинам волн

.

В результате интегрирования найдём:

где с₀=5,67 Вт/(м²·К⁴) — коэффициент излучения абсолютно черного тела. Индекс «О» указывает на то, что рассматривается излучение абсолютно черного тела. Этот закон опытным путем найден Стефаном и теоретически обоснован Больцманом задолго установления закона Планка.

Закон Кирхгофа. Рассмотрим две параллельные поверхности, одна из которых абсолютно черная с температурой Т₀, вторая серая с температурой Т и поглощающей способностью A. Расстояние между поверхностями настолько близко, что испускаемые каждой поверхностью лучи обязательно попадают на противоположную. Серая стенка излучает энергию Е и поглощает часть излучаемой черным телом энергии А·E₀. Излучаемая серым телом энергия Е и отраженная им энергия (1—А)·E₀ попадают на черное тело и поглощаются им.

Результирующее излучение серого тела q_р=Е—А·E₀. При Т₀=Т, q_р=0, отсюда

Итак, отношение излучающей способности серого тела к его поглощающей способности при температурном равновесии не зависит от природы тела и равно энергии излучения абсолютно черного тела при той же температуре. Этот закон справедлив и для монохроматического излучения:

Здесь А_λ — поглощающая способность в узком интервале длин волн. Следовательно, тело, излучающее энергию при какой-либо длине волны, способно поглощать ее при этой же длине волны. На основании равенства (11.17) можно записать Е=А·E₀. Однако по (11.16) Е=ε·E₀. Таким образом, из закона Кирхгофа также следует, что поглощающая способность серого тела численно равна степени его черноты, то есть А=ε.

Закон Ламберта. Определяет изменение энергии излучения по отдельным направлениям. Согласно этому закону, поток излучения абсолютно черного тела в данном направлении, характеризуемый величиной J_φ, пропорционален потоку излучения в направлении нормали к поверхности J_н и косинусу угла между ними, то есть

Гипо́теза Пла́нка — гипотеза, выдвинутая 14 декабря 1900 года Максом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию  , пропорциональной частоте ν излучения:

где h или   — коэффициент пропорциональности, названный впоследствии постоянной Планка. На основе этой гипотезы он предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением — формулу Планка.

Позднее гипотеза Планка была подтверждена экспериментально.

Фотон (от др.-греч. φς, род. пад. φωτς, «свет») — элементарная частица, переносчик электромагнитного взаимодействия, квант электромагнитного поля. Фотоны обозначаются буквой γ, поэтому их часто называют гамма-квантами (особенно фотоны высоких энергий); эти термины практически синонимичны.

29. Фотоэффект. Законы фотоэффекта. Уравнение эйнштейна. В.А.Х.

фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света. В 1900 г. немецкий физик Макс Планк высказал гипотезу: свет излучается и поглощается отдельными порциями — квантами (или фотонами). Энергия каждого фотона определяется формулой Е = hv, где h — постоянная Планка, равная  , v — частота света. Гипотеза Планка объяснила многие явления: в частности, явление фотоэффекта, открытого в 1887 г. немецким ученым Генрихом Герцем и изученного экспериментально русским ученым А. Г. Столетовым. Фотоэффект — это явление испускания электронов веществом под действием света.      В результате исследований были установлены три закона фотоэффекта.     1. Сила тока насыщения прямо пропорциональна интенсивности светового излучения, падающего на поверхность тела.     2. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и зависит от его интенсивности.     3. Если частота света меньше некоторой определенной для данного вещества минимальной частоты, то фотоэффекта не происходит.

Энергия падающего фотона расходуется на совершение электроном работы вы­хода А из металла и на сообщение вылетевшему фотоэлектрону кинетичес­кой энергии mv²_max/2. По закону сохранения энергии,

                                           

Уравнение называется уравнением Эйнштейна для внешнего фотоэффекта.

30. Эффект Комтона. Корпускулярно-волновой дуализм света.

Комптона эффект, комптон-эффект, упругое рассеяние электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны; наблюдается при рассеянии излучения малых длин волн — рентгеновского и гамма-излучения. В К. э. впервые во всей полноте проявились корпускулярные свойства излучения.

 

корпускулярно волновой дуализм света.Первые представления о природе света возникли у древних греков и египтян. По мере изобретения и совершенствования различных оптических приборов (параболических зеркал, микроскопа, зрительной трубы) эти представления развивались и трансформировались. В конце XVII века возникли две теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук и Х. Гюйгенс). Согласно корпускулярной теории, свет представляет собой поток частиц (корпускул), испускаемых светящимися телами. Ньютон считал, что движение световых корпускул подчиняется законам механики. Так, отражение света понималось аналогично отражению упругого шарика от плоскости. Преломление света объяснялось изменением скорости корпускул при переходе из одной среды в другую. Для случая преломления света на границе вакуум–среда корпускулярная теория приводила к следующему виду закона преломления:

где c – скорость света в вакууме, υ – скорость распространения света в среде. Так как n > 1, из корпускулярной теории следовало, что скорость света в средах должна быть больше скорости света в вакууме. Ньютон пытался также объяснить появление интерференционных полос, допуская определенную периодичность световых процессов. Таким образом, корпускулярная теория Ньютона содержала в себе элементы волновых представлений.

31. Корпускулярно-волновой дуализм. Гипотеза де-Бройля. Неопределённость Гейзенберга. Волновые свойства частиц.

Корпускулярно-волновой дуализм — теория в квантовой механике, гласящая, что в зависимости от системы отсчета поток электромагнитного излучения можно рассматривать и как поток частиц (корпускул), и как волну. В частности, свет — это и корпускулы (фотоны), и электромагнитные волны. Свет демонстрирует свойства волны в явлениях дифракции иинтерференции при масштабах, сравнимых с длиной световой волны. Например, одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла.[1]. Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей. Корпускулярные свойства света проявляются при фотоэффекте. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например,электрон).

 Теория де Бройля -  В 1924 г французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновой дуализм имеет универсальный характер. Согласно гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Напомним, что энергия   и импульс   фотона связаны с круговой частотой   и длиной волны   соотношениями

     

     По гипотезе де Бройля движущейся частице, обладающей энергией   и импульсом  , соответствует волновой процесс,

частота которого равна

     

     а длина волны

     

Свойства волн де Бройля. Рассмотрим свойства, которыми обладают волны де Бройля. Прежде всего следует отметить, что волны материи - волны де Бройля - в процессе распространения могут отражаться, преломляться, интерферировать и дифрагировать по обычным волновым законам. Найдем фазовую скорость волн де Бройля  , т.е. скорость, с которой распространяются точки волны с постоянной фазой. Пусть частица движется вдоль оси  , тогда условие постоянства фазы волны (2.3) имеет вид

     

     Дифференцируя это соотношение, находим

     

     Поскольку

     

     где   - релятивистская масса частицы, а   - ее скорость, то для фазовой скорости волны де Бройля получаем следующее выражение

     

принцип неопределённости Гейзенбе́рга (или Га́йзенберга) устанавливает, что существует ненулевой предел для произведения дисперсийсопряжённых пар физических величин, характеризующих состояние системы. Принцип неопределённости обнаруживается также в классической теории измерений физических величин.

Обычно принцип неопределённости иллюстрируется следующим образом. Рассмотрим ансамбль невзаимодействующих эквивалентных частиц, приготовленных в определённом состоянии, для каждой из которых измеряется либо координата q, либо импульс p. При этом результаты измерений будут случайными величинами, среднеквадратические отклонения которых от средних значений будут удовлетворять соотношению неопределённостей  , где   – постоянная Дирака. Поскольку любое измерение изменяет состояние каждой частицы, при одном измерении нельзя одновременно измерить значения и координаты и импульса. Для ансамбля частиц уменьшение дисперсии при измерении физической величины приводит к увеличению дисперсии сопряжённой физической величины. Считается, что принцип неопределённости связан не только с возможностями экспериментальной техники, но и показывает фундаментальное свойство природы.

Волновые свойства частиц. Наиболее отчетливо волновые свойства проявляются у элементарных частиц. Это происходит потому, что из-за малой массы частиц длина волны оказывается сравнимой с расстоянием между атомами в кристаллических решетках. В этом случае при взаимодействии пучка частиц с кристаллической решеткой возникаетдифракция.

Для иллюстрации волновых свойств частиц часто используют мысленный эксперимент – прохождение пучка электронов (или других частиц) через щель ширинойΔx. С точки зрения волновой теории при дифракции на щели пучок будет уширяться с угловой расходимостью θ ≥ λ / Δx. С корпускулярной точки зрения уширение пучка после прохождения щели объясняется появлением у частиц некоторого поперечного импульса. Разброс значений этого поперечного импульса («неопределенность») есть 

Δpx ≈ pθ ≥ (λ / Δx)p = h / Δx.

Соотношение 

Δpx · Δx ≥ h

носит название соотношения неопределенностей. Это соотношение на корпускулярном языке выражает наличие волновых свойств у частиц.

Эксперимент по прохождению пучка электронов через две близко расположенные щели может служить еще более яркой иллюстрацией волновых свойств частиц. Этот эксперимент является аналогом оптического интерференционного опыта Юнга.

Компьютерная модель воссоздает на экране дисплея мысленные эксперименты по дифракции электронов на одной и двух щелях.

Подлетая к экрану со щелями, частицы взаимодействуют с ним как волны де Бройля. Поведение частиц в пространстве между экраном со щелями и фотопластинкой описывается в квантовой физике с помощью Ψ-функций. Квадрат модуля пси-функции определяет вероятность обнаружения частицы в том или ином месте. Таким образом, попадание частиц в различные точки фотопластинки есть вероятностный процесс. Компьютерная модель позволяет продемонстрировать этот процесс.

В случае одиночной щели модель иллюстрирует соотношение неопределенностей, которое является следствием двойственной природы частиц. Можно изменять в некоторых пределах ширину щели и наблюдать дифракционное размытие электронного пучка на фотопластинке.

Предполагается, что электроны имеют энергию порядка 100 эВ.

Обратите внимание, что в случае двух щелей наблюдаемое на фотопластинке распределение не является простым наложением двух независимых распределений от каждой из щелей в отдельности. Появление интерференционных полос на фотопластинке однозначно свидетельствует о том, что каждая достигшая фотопластинки частица одновременно прошла через обе щели экрана.

32.Волновая функция и её физический смысл. Уравнение Шрёдингера для стационарных состояний.

Волновая функция и ее физический смысл.

 

Из содержания предыдущих двух параграфов следует, что с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, поэтому состояние частицы в квантовой механике описывают волновой функцией, которая зависит от координат и времени (x,y,z,t). Конкретный вид -функции определяется состоянием частицы, характером действующих на нее сил. Если силовое поле, действующее на частицу, является стационарным, т.е. не завися­щим от времени, то -функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой  – откоординат:

             (3.1)

В дальнейшем будем рассматривать только стационарные состояния. -функция является вероятностной характеристикой состояния частицы. Чтобы пояснить это, мысленно выделим достаточно малый объем  , в пределах которого значения -функции будем считать одинаковыми. Тогда вероятность нахождения dW частицы в данном объ­еме пропорциональна ему и зависит от квадрата модуля-функции (квадрата модуля амплитуды волн де Бройля):                             

                                     (3.2)

Отсюда следует физический смысл волновой функции:

.                                              (3.3)

Квадрат модуля волновой функции имеет смысл плотности вероят­ности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Интегрируя выражение (3.2) по объему, определяем вероятность нахождения частицы в этом объеме в условиях стационарного поля:

                                               (3.4)

Если известно, что частица находится в пределах объема V, то инте­грал выражения (3.4), взятый по объему V, должен быть равен единице: 

                                                         (3.5)

– условие нормировки -функции.

Чтобы волновая функция являлась объективной характеристикой со­стояния микрочастиц, она должна быть конечной, однозначной, непре­рывной, так как вероятность не может быть больше единицы, не может быть неоднозначной величиной и не может изменяться скачками. Таким образом, состояние микрочастицы полностью определяется волновой функцией. Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля.

 

Уравнение Шредингера для стационарных состояний

В стационарном случае уравнение Шредингера имеет вид

 

где Е, U - полная и потенциальная энергия, m - масса частицы.

33. Квантование энергии. Частица в потенциальной яме. Прохождение частицы через потенциальный барьер. Туннельный эффект.

Квантование энергии. Некоторые физические величины, относящиеся к микрообъектам, изменяются не непрерывно, а скачкообразно. О величинах, которые могут принимать только вполне определенные, то есть дискретные значения (латинское "дискретус" означает разделенный, прерывистый), говорят, что они квантуются.

В 1900 г. немецкий физик М. Планк, изучавший тепловое излучение твердых тел, пришел к выводу, что электромагнитное излучение испускается в виде отдельных порций - квантов - энергии. Значение одного кванта энергии равно

ΔE = hν,

где ΔE - энергия кванта, Дж; ν - частота, с^-1; h - постоянная Планка (одна из фундаментальных постоянных природы), равная 6,626·10⁻³⁴ Дж·с.  Кванты энергии впоследствии назвали фотонами.

Частица в потенциальной яме. Простой физической моделью финитного движения может служить движение частицы в одномерной «потенциальной яме» с бесконечно высокими стенками. Частица не может покинуть область размером L. Она движется в этой области, испытывая многократные отражения от стенок. С волновой точки зрения между стенками во встречных направлениях движутся две волны де Бройля. Это напоминает картину двух встречных волн, бегущих по струне с закрепленными концами. Как и в случае струны, стационарным состояниям соответствуют стоячие волны, которые образуются при условии, что на длине L укладывается целое число полуволн: 

L = n · (λ / 2)   (n = 1, 2, 3, ...)

Таким образом, стационарным состояниям частицы, запертой в потенциальной яме, соответствует дискретный набор длин волн. Поскольку в квантово-механическом случае длина волны λ однозначно связана с импульсом частицы: λ = h / p, а импульс частицы определяет энергию ее движения: E = p² / (2m)(нерелятивистское приближение), то квантованной оказывается и энергия частицы. Квантово-механический расчет приводит к следующему выражению: 

Здесь m – масса частицы, h – постоянная Планка, E₁ = h² / (8mL²) – энергия наинизшего состояния.

Следует обратить внимание, что квантово-механическая частица в отличие от классической не может покоиться на дне потенциальной ямы, то есть иметь энергию E₁ = 0. Это противоречило бы соотношению неопределенностей 

Δx · Δpx ≥ h.

Действительно, у покоящейся частицы импульс строго равен нулю, следовательно, Δp_x = 0. В то же время неопределенность координаты частицы Δx ≈ L. Поэтому произведение Δx · Δp_x у частицы, лежащей на дне потенциальной ямы, должно было бы равняться нулю.

Соотношение неопределенностей позволяет сделать оценку минимальной энергии E₁ частицы. Если принять, что в состоянии с минимальной энергией p_x ≈ Δp_x, то для минимальной энергии E₁ получается выражения 

Прохождение частицы через потенциальный барьер. Если мы имеем две области пространства, в которых потенциальная энергия частицы меньше, нежели на поверхности, раз­деляющей эти области, то мы говорим, что области разделены потенциальным барьером.

Простейшим примером потенциального барьера может служить барьер в одном измерении, изображенный на рис.1. По оси ординат отложена потенциальная энергия U (х) в функции коор­динаты частицы х. В точке х₀ потенциальная энергия имеет мак­симум U_m. Все пространство - ∞ < Х < + ∞ делится в этой точке на две области; х < х₀ и х > х₀ , в которых U<U_m. Зна­чение термина «потенциальный барьер» сейчас же выяснится, если мы рассмотрим, движение частицы в поле U (х) на основе классической механики. Полная энергия частицы E равна

(1)

где р —импульс частицы, а μ – её масса. Решая (1) относительно импульса, получим

(2)

Знаки ± следует выбрать в зависимости от направления движе­ния частицы. Если энергия частицы Е больше «высоты» барьера U_m, то частица беспрепятственно пройдет барьер слева направо, если начальный импульс р>0, или в противоположном направлении, если начальный импульс р < 0.

Допустим, что частица движется слева, имея полную энергию Е, меньшую U _т. Тогда в некоторой точке x_t потенциальная энергия U (х₁)=Е, p(x₁)=0, частица остановится. Вся ее энер­гия обратится в потенциальную, и движение начнется в обратном порядке: х₁ есть точка поворота. Поэтому при E<.U_m частица, движущаяся слева, не пройдет через область максимума потенциала (х = х₀) и не проникнет во вторую область х > х₀ Подобным же образом, если частица движется справа налево, имея Е < U_m , то она не проникнет в область за второй точкой поворота х₂,

Рис. 1.1. Потенциальный барьер в одном измерении.	Рис. 1.2. Самый простой потенциальный барьер

в которой U(x₂)=E (рис.1). Таким образом, потенциальный барьер является «непрозрачной» перегородкой для всех частиц, энергия которых меньше U_m (напротив, он «прозрачен» для частиц, обладающих энергией Е >U_m). Этим и разъясняется название «потенциальный барьер».

Совсем иначе протекают явления вблизи потенциальных барьеров, если речь идет о движениях микроскопических частиц в микроскопических полях, т. е. о движениях, при рассмотрении которых нельзя игнорировать квантовые эффекты. В этом случае, как мы сейчас увидим, в противоположность выводам классической механики, частицы с энергией Е, большей высоты барьера U_m, частично отражаются от барьера, а частицы с энергией, меньшей U_m, частично проникают через барьер.

ТУННЕЛЬНЫЙ ЭФФЕКТ, квантовый эффект, состоящий в проникновении квантовой частицы сквозь область пространства, в которой согласно законам классич. физики нахождение частицы запрещено. Классич. частица, обладающая полной энергией E и находящаяся в потенц. поле, может пребывать лишь в тех областях пространства, в которых ее полная энергия не превышает потенц. энергию U взаимодействия с полем. Поскольку волновая ф-ция квантовой частицы отлична от нуля во всем пространстве и вероятность нахождения частицы в определенной области пространства задается квадратом модуля волновой ф-ции, то и в запрещенных (с точки зрения классич. механики) областях волновая ф-ция отлична от нуля
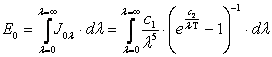