
Часть с.
С1.
![]()
![]()
С2.
Сколько различных корней имеет уравнение
(4x
– x2
- 3) ∙ ![]() = 0 ?
= 0 ?
Вариант № 9. Часть а.
А1. Упростите выражение n20 : n5.
1) n15 2) 15n3 3) 15n-2,5 4) n4
A2.
Вычислите
![]() +
+ ![]() 8.
8.
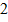 2)
2)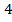 3)
4)2 + 5
3)
4)2 + 5 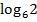
А3.Вычислите
![]() .
.
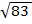 2)
3)
2)
3)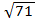 4)
9
4)
9
A4. На одном из следующих рисунков изображен график четной функции. Укажите номер этого рисунка.
A5. Найдите производную функции y = ex- x3.
1) y’ = 4xex-1 – 21x2 2) y’ = ex – x3 3) y’ = ex – 3x2 4) y’ = x – x3
A6. Решите неравенство 71+x ≤ 73
1) (-∞; 2] 2) (-∞; 2) 3) (-∞; -1) U (3; +∞) 4) (0; 1)
A7. Решите уравнение 2 sin x = 1.
1)
![]() 2) (-1)n
2) (-1)n
![]() + πn,
nЄZ
3)
+ πn,
nЄZ
3)![]() 4)
(-1)n
+ 2πn,
nЄZ
4)
(-1)n
+ 2πn,
nЄZ
A8. Решите неравенство log3(5x - 12) > 1.
1) (-∞; 1) 2) (1; +∞) 3) (3; +∞) 4) [3; +∞)
А9. Решите неравенство 73х+2 > 75.
1) (-∞; 1) 2) (1; +∞) 3) (0; +∞) 4) [0; +∞)
A10.
Решите неравенство ![]() < 0.
< 0.
1) (-∞; -1) U (4; 6) 2) (-1; 2) U (4; +∞) 3) (-∞; -1) U (2; 4) 4) (-∞; -1) U (4; +∞)
Часть в.
B1.
Найдите значение выражения ![]()
![]() если
если
![]() =
=![]() ,
π
≤
,
π
≤ ![]() ≤
≤
![]() .
.
B2. Решите уравнение sin2 x – 3 sin x + 2 = 0. В ответе укажите наименьший положительный корень.
B3.
Решите уравнение ![]() =
=
![]() -
- ![]()
B4.
Решите уравнение: 72x
–48 · ![]() x
–
49 = 0. Если уравнение имеет более одного
корня, то в ответе укажите их сумму.
x
–
49 = 0. Если уравнение имеет более одного
корня, то в ответе укажите их сумму.
B5. Зависимость пути от времени при прямолинейном движении тел задана уравнениями:
S1(t)
=
t3
+ 2 t2
– 45 S2(t)
= ![]() t2
+ 4 t
+ 115
t2
+ 4 t
+ 115
В какой момент времени скорости их движения будут равными?
B6.
Вычислите значение выражения ![]() +
+
![]() .
.
В7. Функция определена на промежутке . На рисунке изображен график ее производной. Найдите разность точек минимума функции.
B8. Сколько литров уксусной кислоты в 50 л 9% уксуса?
B9.
Решите
неравенство ![]() ≥ 1. В ответе укажите наименьший
положительный корень.
≥ 1. В ответе укажите наименьший
положительный корень.
B10. Найти площадь поверхности прямоугольного параллелепипеда, если стороны основания 2 и 3, высота 4.
Часть с.
С1.
![]()
С2.
Сколько различных корней имеет уравнение
(6x
– 6) · ![]() =
0 ?
=
0 ?
Вариант № 10.
Часть а.
А1. Упростите выражение: m12: m6 .
1) 15m1,5 2) 3,25m 3) m2 4) m6
A2.
Вычислите: ![]() +
+ ![]()
1)![]() 2)
2)![]() 3)
3)![]() 4) 4
4) 4
А3.
Вычислите: ![]() ·
·
![]() .
.
2 2) 3)
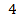 4)
4)
A4. На одном из следующих рисунков изображен график нечетной функции. Укажите номер этого рисунка.
A5. Найдите производную функции y = 3 sin x + 2 cos x.
1) y’ = 3 cos x + 2 sin x 2) y’ = 3 cos x - 2 sin x
3) y’ = -3 cos x - 2 sin x 4) y’ = -3 cos x +2 sin x
A6. Найдите множество значений функции y = 7 + 5 sin x.
1) [4; 10] 2) [6; 8] 3) [2; 12] 4) [4; 7]
A7.
Решите уравнение 3 tg
x
= ![]()
1)
![]() 2) (-1)n
2) (-1)n
![]() + 2πn,
nЄZ
3)
+ 2πn,
nЄZ
3)![]() 4)
4)
![]() + πn,
nЄZ
+ πn,
nЄZ
A8. Решите неравенство log11(7 + x) > 1
1) (-∞; 7) 2) (1; +∞) 3) (4; +∞) 4) [4; +∞)
A9. Решите неравенство 3x-2 ≤ 36-x
1) (-∞; 4] 2) (-∞; 4) 3) (-4; +∞) 4) [-4; +∞)
A10.
Решите неравенство ![]() > 0.
> 0.
1) (-∞; -2) U (1; 4) 2) (-2; 1) U (3; +∞) 3) (-∞; 1) U (3; 4) 4) (-2; 1) U (4; +∞)
