
Вариант № 6. Часть а.
А1.Упростите выражение: (5a-2)2.
1)![]() 2)
2)![]() 3)
3) ![]() 4)
4)![]()
А2.
Вычислите ![]()
1)![]() 2) 8 3) 64 4)
2) 8 3) 64 4)![]()
A3.
Вычислите ![]() 8
+
2.
8
+
2.
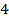 2)
2)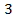 3)
3)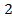 4) 16
4) 16
A4. На одном из следующих рисунков изображен график нечетной функции. Укажите номер этого рисунка.
A5. Найдите производную функции y = x4 + cos x.
1)
y’ = 4x3
- sin x 2) y’ = ![]() + sin x 3) y’ =
- sin x 4) y’ = 4x3
+ sin x
+ sin x 3) y’ =
- sin x 4) y’ = 4x3
+ sin x
A6. Найдите множество значений функции y = 2,1 cos x.
1) [-1; 5] 2) [-1; 1] 3) [2; 4] 4) [-2,1; 2,1]
A7. Решите уравнение 2 cos x = 1.
1)![]() + 2πn,
nЄZ
2)
+ 2πn,
nЄZ
2)![]() n,
nЄZ
3)
n,
nЄZ
3) ![]() + πn,
nЄZ
4)
+ 2πn,
nЄZ
+ πn,
nЄZ
4)
+ 2πn,
nЄZ
A8. Решите уравнение: log7(3x +4) =1.
1) 1 2) 11 3) -1 4) 0
A9. Решите неравенство 5x-2 ≤ 5 -1
1) (-∞;1] 2)(- ∞; -2) U (-1; +∞) 3) [1; +∞) 4) (- ∞; -2) U (-1; +∞)
A10.
Решите неравенство ![]() < 0.
< 0.
1) (-9; 3) U (3; +∞) 2) (- ∞; -9) U (2; 3) 3) (-9; 2) U (3; +∞) 4) (- ∞; -2) U (2; 3)
Часть в.
B1.
Найдите значение выражения ![]() , если cos
, если cos
![]() =
= ![]() ,
,
![]()
![]() ≤
≤ ![]() ≤
2π.
≤
2π.
B2. Решите уравнение cos2 x – 3 cos x - 4 = 0. В ответе укажите наименьший положительный корень уравнения.
B3.
Решите уравнение:![]() 5
·
5
· ![]() = 1,5 + 3x.
= 1,5 + 3x.
B4.
Решите уравнение ![]() +
3
+
3![]() - 18 = 0. Если уравнение имеет более одного
корня, то в ответе укажите их произведение.
- 18 = 0. Если уравнение имеет более одного
корня, то в ответе укажите их произведение.
B5.
Зависимость пути от времени при
прямолинейном движением точки задана
уравнением S(t)
= ![]() t3
+ 2t2
– 3. Вычислите ее скорость в момент
времени t
= 4c.
t3
+ 2t2
– 3. Вычислите ее скорость в момент
времени t
= 4c.
B6.
Вычислите значение выражения ![]() +
+
![]() .
.
В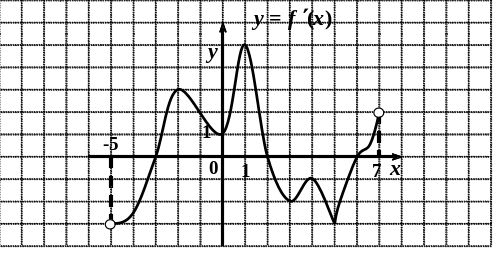 7.Функция
7.Функция
![]() определена на промежутке
определена на промежутке
![]() .
На рисунке изображен график ее производной.
Найдите точку максимума функции.
.
На рисунке изображен график ее производной.
Найдите точку максимума функции.
B8. При сушке грибы теряют 80% массы. Какова будет масса 10 кг грибов после сушки?
B9.
Решите неравенство: ![]() > 16. В ответе запишите наименьший
положительный целочисленный корень.
> 16. В ответе запишите наименьший
положительный целочисленный корень.
B10.
Найти оббьем шара, если его радиус равен
![]() .
.
Часть с.
С1.
![]()
C2.
Решите уравнение (2x-3)
∙ ![]() = 0.
= 0.
Вариант № 7. Часть а.
А1.
Упростите выражение 3a-1
![]() 4а2.
4а2.
1)![]() 2)
2)![]() 3)
3) ![]() 4) 12a
4) 12a
А2.
Вычислите: ![]() ∙
∙ ![]()
1)![]() 2)27 3)18 4)
2)27 3)18 4)![]()
A3.
Вычислите: ![]() 75
-
3.
75
-
3.
1)![]() 2)
3)
2)
3)![]() 4) 25
4) 25
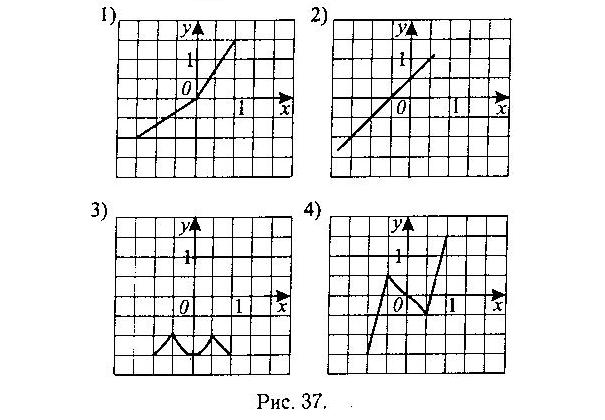
A4. На одном из следующих рисунков изображен график четной функции. Укажите номер этого рисунка.
A5.Найдите производную функции y = ex+ 3 x3.
1) -ex+ 3 x3 2) -xex+ 9 x2 3) ex+ 9 x2 4) -ex-1+ 9 x3
A6.
Решите уравнение ![]() =
4o.
=
4o.
1)![]() 2) 1 3) 2
4)
2) 1 3) 2
4)
A7.Решите
уравнение sin
x
= ![]()
1)![]() 2)
2)![]() 3)(-1)n
3)(-1)n
![]() + 2πn,
nЄZ
4) (-1)n
∙
+ 2πn,
nЄZ
4) (-1)n
∙ ![]() + πn,
nЄZ
+ πn,
nЄZ
A8. Решите неравенство log2 (2x+4) < 1.
1) (-∞; 1) 2) (-∞; -1) 3) (-2;-1) 4) (-2;1)
A9. Решите неравенство 10x+1≥ 102.
1) (1: +∞) 2) (-∞; 2) 3) [1; +∞) 4)(2; +∞)
A10.Решите
неравенство ![]() ≥ 0.
≥ 0.
1) (-∞; -0,5] U (2; 5] 2) [-0,5; 2) U [5; +∞) 3) [-0,5; 5] 4) (- ∞; -0,5) U (2; +∞)

