16. Уравнение с полным дифференциалом

Пусть имеется дифференцируемая функция двух переменных . Ее дифференциал имеет вид 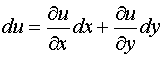. Если известно, что  во всей области определения функции , то функция является тождественной константой: . Если же имеется некоторая функция , то, очевидно, что .

Таким образом, если дифференциальное уравнение первого порядка имеет вид

  , (1)

где ,  - некоторые функции, то, убедившись, что левая часть уравнения (1) есть дифференциал некоторой функции , можно записать общий интеграл уравнения

  . (2)

Для того, чтобы левая часть уравнения (1) являлась полным дифференциалом некоторой функции  необходимо и достаточно, чтобы

  , (3)

поскольку если , то 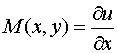, , 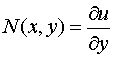а условие (3.3) – не что иное, как равенство .

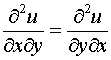Так как 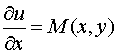, то

  .  (4)

Функцию  найдем, дифференцируя равенство (4) по переменной :

  .

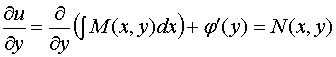Пример 1. Решить дифференциальное уравнение

  .

Решение. Данное уравнение имеет вид (1), где

  , .

Проверим выполнение условия (3):

  ,

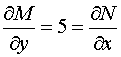следовательно, данное уравнение есть уравнение в полных дифференциалах. Следовательно,

  , ,

  ,

  .

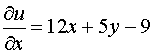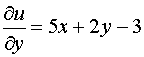Дифференцируем полученное равенство по :

  ,

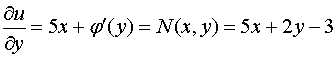 откуда .

Решим полученное дифференциальное уравнение

  ,

Получим .

Общий интеграл уравнения имеет вид

  , то есть

  .

Если левая часть уравнения (1) не является полным дифференциалом, то можно подобрать (если это удается) функцию , поле умножения на которую левая часть уравнения (1) обращается в полный дифференциал:

  . (5)

Функция  называется интегрирующим множителем. Существование интегрирующего множителя было доказано Эйлером, который указал ряд классов дифференциальных уравнений с интегрирующими множителями заданного вида. Надо заметить, что подбор интегрирующего множителя требует некоторой изобретательности.

Пример 2. Решить дифференциальное уравнение

  .

Решение. Домножим обе части уравнения на интегрирующий множитель :

  ,

  .

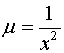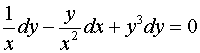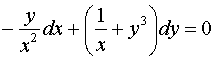Получили уравнение вида (1), где , . Проверим выполнение условия (3):

  ; .

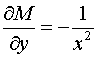Таким образом, после введения интегрирующего множителя получен полный дифференциал некоторой функции , где , .

  ,

  .

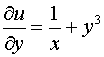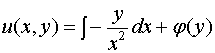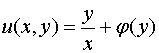Продифференцируем полученное выражение по переменной :

  .

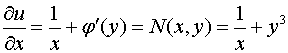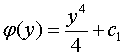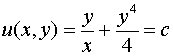Поскольку , то , а искомая функция  или .