10. Частные производные

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции определяется следующим образом:

Следует обратить внимание, что обозначение следует понимать как цельный символ, в отличие от обычной производной функции одной переменной , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции: , где  — частный дифференциал функции f по переменной x. Часто непонимание факта цельности символа является причиной ошибок и недоразумений, как, например, сокращение в выражении . (подробнее см. Фихтенгольц, «Курс дифференциального и интегрального исчисления»).

Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции в точке по координате равна производной по направлению , где единица стоит на -ом месте.

Примеры

Объём V конуса зависит от высоты h и радиуса r, согласно формуле

Частная производная объема V относительно радиуса r

которая показывает скорость, с которой изменяется объем конуса, если его радиус меняется, а его высота остается неизменной. Частная производная относительно h

которая показывает скорость, с которой изменяется объем конуса, если его высота меняется, а его радиус остается неизменным.

Полная производная V относительно r и h

и

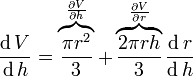
Различие между полной и частной производной — устранение косвенных зависимостей между переменными в последней.

Если (по некоторым причинам) пропорции конуса остаются неизменными, то высота и радиус находятся в фиксированном отношении k,

Это дает полную производную относительно r:

Уравнения, в которые входят частные производные, называются дифференциальными уравнениями в частных производных и широко известны в физике, инженерии и других науках и прикладных дисциплинах.

10. Двойной интеграл и сведение его к повторному

     Излагаемое далее сведение двойного интеграла к повторному однократному является одним из эффективных способов вычисления двойного интеграла.

1. Случай прямоугольника

     Теорема 6. Пусть для функции f(x, y) в прямоугольнике R = [a ≤ x ≤ b] × [c ≤ y ≤ d] существует двойной интеграл .

     Пусть далее для каждого x из сегмента a ≤ x ≤ b существует однократный интеграл

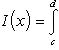
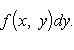     (12)

Тогда существует повторный интеграл

и справедливо равенство

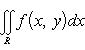
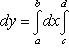
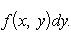     (13)

     Доказательство. Разобъем прямоугольник R с помощью точек a = x₀ < x₁ < x₂ < ... < x_n = b и c = y₀ < y₁ < y₂ < ... < y_p = d на n · p частичных прямоугольников

R_kl = [x_k-1 ≤ x ≤ x_k] × [y_l-1 ≤ y ≤ y_l] (k = 1, 2, ..., n; l = 1, 2, ..., p).

Положим Δx_k = x_k - x_k-1, Δy_l = y_l - y_l-1 и обозначим через M_kl и m_kl точные грани функции f(x, y) на частичном прямоугольнике R_kl. Тогда всюду на этом прямоугольнике

m_kl ≤ f(x, y) ≤ M_kl.     (14)

     Положим в этом неравенстве x = ξ_k, где ξ_k - произвольная точка сегмента [x_k-1, x_k], и после этого проинтегрируем (14) по y в пределах y_l-1 до y_l. Получим

     (15)

Суммируя (15) по всем l от 1 до p и используя обозначение (12), будем иметь

     (16)

Далее умножим (16) на Δx_k и просуммируем по всем k от 1 до n. Получим

     (17)

     Пусть наибольший диаметр Δ частичных прямоугольников стремится к нулю. Тогда и наибольшая из длин Δx_k стремится к нулю. Обрамляющие члены в (17), представляющие собой нижнюю и вернюю суммы, стремятся при этом к двойному интегралу .

     Стало быть, существует предел и среднего члена в (17), равный тому же самому двойному интегралу. Но этот предел по определению однократного интеграла равен

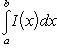
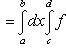
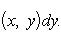
Тем самым доказано существование повторного интеграла и равенство (13). Теорема доказана.

     Замечание. В теореме 6 можно поменять x и y ролями, т. е. моно предположить существование двойного интеграла и существование для любого y из сегмента c ≤ y ≤ d однократного интеграла

Тогда теорема будет утвердать существование повторного интеграла

и равенство

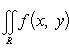
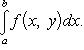     (18)

 Случай произвольной области

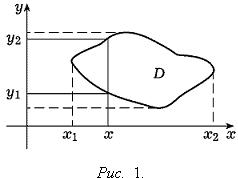
     Теорема 7. Пусть выполнены следующие условия: 1) область D ограничена, замкнута и такова, что любая прямая, параллельная оси Oy, пересекает границу этой области не более чем в двух точках, ординаты которых суть y₁(x) и y₂(x), где y₁(x) ≤ y₂(x) (см. Рис. 1); 2) функция f(x, y) допускает существование двойного интеграла

и существование для любого x однократного интеграла

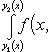
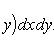
     При этих условиях существует повторный интеграл

(x₁ и x₂ - наименьшая и наибольшая абсциссы точек области D) и справедливо равенство

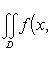
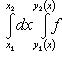
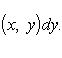     (19)

     Доказательство. Обозначим через R прямоугольник со сторонами, параллельными координатным осям, содержащий область D, а через F(x, y) - функцию, совпадающую с f(x, y) в точках области D и равную нулю в остальных точках R. Для функции F(x, y) в прямоугольнике R выполнены все условия теоремы 7, и, стало быть, справедлива формула (13), которая (с учетом того, что F(x, y) равна нулю вне D и совпадает с f(x, y) в D) переходит в формулу (19). Теорема доказана.

  Замечание 1. В теореме 7 можно поменять ролями x и y, т. е. можно предположить, что выполнены следующие два условия: 1) область D такова, что любая прямая, параллельная оси Ox, пересекает границу этой области не более чем в двух точках, абсциссы которых x₁(y) и x₂(y), где x₁(y) ≤ x₂(y) (см. Рис. 2); 2) функция f(x, y) допускает существование по области D двойного интеграла и существование для любого y однократного интеграла

     При выполнении этих двух условий существует повторный интеграл

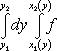
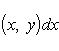
(y₁ и y₂ - наименьшая и наибольшая ординаты точек области D) и справедливо равенство

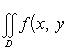
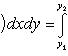
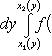
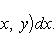     (19')

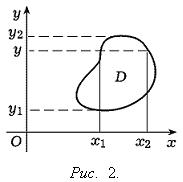
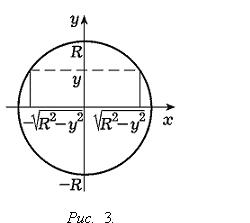
     Пример. Пусть область D - круг x² + y² ≤ R² (см. Рис. 3), а f(x, y) = x²(R² - y²)^3/2. Любая прямая, параллельная оси Ox, пересекает границу D не более чем в двух точках, абсциссы которых и (см. Рис. 3). Поэтому применяя формулу (19'), получим

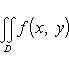
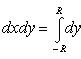
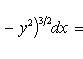
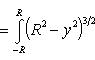
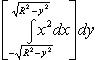
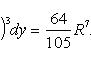
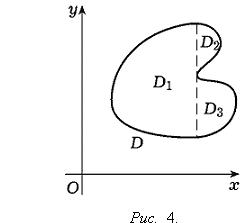
     Замечание 2. В случае, если область D не удоволетворяет требованиям теоремы 7 или замечания 1 к этой теореме, часто удается разбить эту область на сумму конечного числа областей такого типа, не имеющих общих внутренних точек. Тогда интеграл по области D, в силу свойства аддитивности, равен сумме интегралов по соответствующим областям. Так, область D, изображенную на Рис. 4, удается разбить на сумму трех областей D₁, D₂ и D₃, к каждой из которых применима теорема 7 или замечание 1.