3. Формула Ньютона-Лейбница

4. Вычисление определённого интеграла по частям и с заменой переменной

 Замена переменного (интегрирование подстановкой)

     Если функция x = x(u) непрерывно дифференцируема на интервале , а функция f(x) непрерывна на интервале , где m - точная нижняя, а M - точная верхняя граница функции x(u) на интервале , то

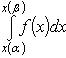
5. Понятие числового ряда и его суммы

Числовым рядом (ч. р.) называется выражение, полученное последовательным сложением членов числовой последовательности т.е. й частичной суммой ряда называется

Ряд называется сходящимся, если существует конечный предел являющийся суммой ряда; расходящимся, если Числа — члены ряда, — й или общий член.

Коротко ряд записывают

Примеры: 1.— гармонический

ряд;

2. — геометрическая прогрессия, где q — знаменатель прогрессии.

Выясним сходимость геометрической прогрессии. Из курса элементарной математики известно, что т.е.

При q = 1 рад принимает вид

при q = -1 геометрическая прогрессия имеет вид

т.е. = 0 при п четном и = а при n нечетном. Таким образом, по определению, геометрическая прогрессия сходится при 1 и расходится при

6. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами

Признак Даламбера:

Пусть дан знакоположительный числовой ряд

(7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство:

По условию существует предел . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие

или p-E< (10)

Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем … или

или

(11)

Рассмотрим ряды:

(12)

. (13)

Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.

Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтому un¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.

 

Замечания:

1. Если расходимость ряда установлена с помощью признака Даламбера, то un¹0.

2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.

3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.

Признак Коши:

Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство:

По условию существует Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | | <E или

p-E< <p+E. (14)

Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <q или un<qn для всех n³N. Рассмотрим ряды

(15)

(16)

Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).

Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или un>1, следовательно, un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.