Получим дифференциальное уравнение регулятора в приращениях и в размерной форме записи:

. (3.26)

В безразмерной форме уравнение имеет вид

. (3.27)

Здесь принято обозначение

.

Коэффициент k_p называется коэффициентом усиления регулятора, а коэффициенты Т₂² и Т₁ имеют размерности соответственно квадрата и первой степени времени. Такое обозначение логично и удобно.

Решение уравнения звена второго порядка.

В результате решения мы получим закон изменения во времени выходной величины регулятора x. Примем, как это уже стало привычным, что входная величина изменяется скачкообразно:

t  0 , y = 0 ; t  0 , y = y₀ = const.

Решение уравнения (3.27) ищется в форме

x = + ,

где – общее решение соответствующего однородного уравнения

, (3.28)

– частное решение уравнения (3.27).

По аналогии со случаем, рассмотренным в разделе “объект регулирования”, частное решение как новое установившееся значение выходной величины будет

.

Общее решение уравнения (28) ищется в форме

,

где C₁ и C₂ – постоянные интегрирования, p₁ и p₂ – корни характеристического уравнения

. (3.29)

Таким образом,

. (3.30)

Постоянные интегрирования, как и в случае объекта регулирования, определим на основании начальных условий. Исходный установившийся режим характеризуется следующими условиями:

t = 0; x = 0; . (3.31)

Подстановка (3.31) в (3.30) даёт

. (3.32)

Отсюда постоянные интегрирования

; , (3.33)

и окончательно

. (3.34)

Частные случаи.

В зависимости от вида корней характеристического уравнения (вещественные, комплексные либо чисто мнимые) имеется три частных случая. Обратим, однако, внимание на то, что решение уравнения (3.27) в форме (3.34) получено для общего случая, независимо от вида корней.

6.А.В случае, когда выполняется условие

характеристическое уравнение имеет два вещественных отрицательных корня

,

и переходный процесс описывается формулой

. (3.35)

Соответствующий график переходного процесса показан на рис. 3.9. Звено в этом случае называется апериодическим звеном второго порядка, чем подчёркивается факт отсутствия колебаний в переходном процессе.

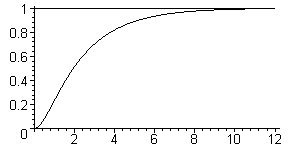
Рис. 3.9. Переходный процесс апериодического звена 2 порядка

6.Б. В случае, когда

,

корни характеристического уравнения комлексно-сопряжённые с отрицательной вещественной частью:

.

Подстановка этих значений в выражение (34) с учётом того, что, согласно формуле Эйлера,

e ^±it =cost ± isint ,

после простых преобразований приводит к такому результату:

. (3.36)

График переходного процесса для этого случая показан на рис. 3.10. Звено называется колебательным, и период колебаний выражается через частоту свободных колебаний так:

T_кол = 2/. (3.37)

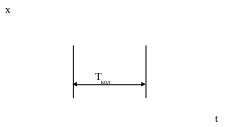
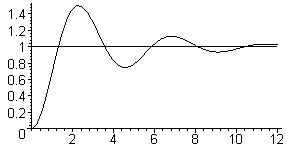
Рис. 3.10. Переходный процесс колебательного звена