19

I. Неопределенный интеграл

В курсе дифференциального исчисления рассматривалась операция дифференцирования как операция перехода от функции к функции, где производная. На основании формулы при этом решается задача нахождения дифференциала функции. Рассмотрим теперь обратные операции, осуществляющие переход от функциик функциии от дифференциалак функции.

Определение 1. Пусть функция определена на некотором конечном или бесконечном промежуткечисловой оси. Функция, определенная на этом же промежутке, называется первообразной функцией (или просто первообразной) функциина, если:

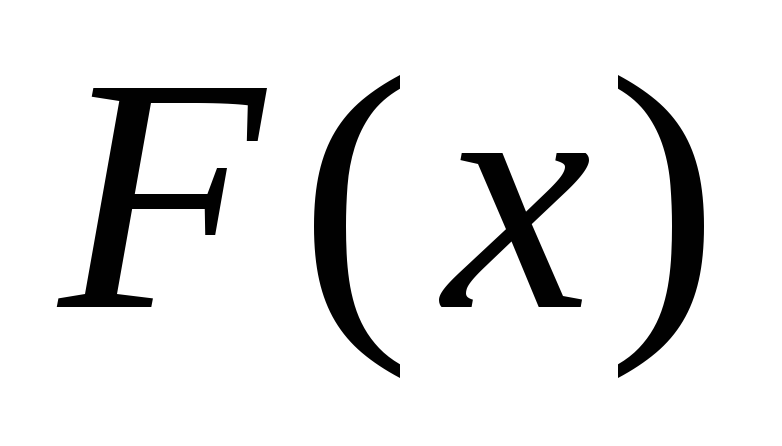1. непрерывна на ;

2) во всех внутренних точках промежуткафункцияимеет производную, а дифференциальное выражениеслужит длядифференциалом, т. е..

Соотношение определяетнеоднозначно. Так, например, равенствопоказывает, чтоявляется первообразной функции. В то же время справедливо равенство, из которого следует, чтоявляется первообразной той же самой функции. При этом первообразныеиотличаются на постоянную:

.

Это свойство первообразных можно доказать и в общем случае:

Т е о р е м а. Пусть и первообразные для на. Тогда найдется постоянная, такая, что всюду на этом интервале.

Определение 2. Совокупность всех первообразных функции , определенных на некотором промежутке, называется неопределенным интегралом отна этом промежутке и обозначается через.

Символ называется знаком интеграла, подынтегральной функцией. Интервал обычно является интервалом непрерывности функциии поэтому при записи неопределенного интеграла не указывается. Из приведенной теоремы и определения 2 следует, что функции из совокупности функцийотличаются друг от друга на постоянную. Поэтому, если какая-либо первообразная, то можно записать равенство , где постояннаяпробегает множество действительных чисел. Таким образом, фигурные скобки обозначают совокупность функций. Для краткости записи фигурные скобки опускают и пишут.

Выше мы определили неопределенный интеграл от функции . Теперь определим неопределенный интеграл от дифференциала.

Определение 3. Неопределенным интегралом от дифференциала на промежуткеназывается совокупность всех первообразных для функциина этом промежутке. Он, как и неопределенный интеграл от функции, обозначается символом.

Если на, то по свойству дифференциала последний под знаком интеграла можно записать в одном из следующих видов:.

Неопределенный интеграл от дифференциала и неопределенный интеграл от функции задают одну и ту же совокупность функций. Поэтому оставим для них общее обозначение. Из контекста будет ясно, о каком из неопределенных интегралов идет речь. Переменнаяуказывает, от какой переменой зависит соответствующая совокупность первообразных, поэтому.

Нахождение первообразной или вычисление неопределенного интеграла в основном состоит в преобразовании подынтегрального выражения таким образом, чтобы получить следующие табличные интегралы:

; );;

; ;

; ;

; ;

;

; ;

; ;

;

.

Эти формулы проверяются непосредственным дифференцированием. Справедливы также следующие правила вычисления неопределенных интегралов:

1. ;

2. .

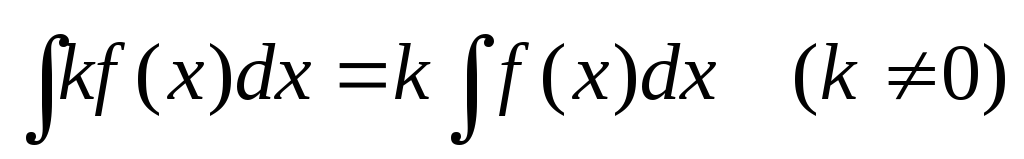При вычислении неопределенных интегралов от дифференциалов оказываются полезными следующие равенства:

Для каждой из формул ясно, на каком промежутке она справедлива.

Непосредственным вычислением можно проверить, что

. Поэтому для случая интеграла от дифференциала справедливо:

3) .

Пример

. .

Обозначение часто опускают, когда ясно, о какомидет речь. Так, например:

.

.

При сведении интегралов к табличным иногда используются такие тождества:

,

, .

Пример

.

.

.

Для дифференциала в случае непрерывно дифференцируемых функций иимеет место равенство. С помощью этого равенства можно установить важное для непосредственного интегрирования правило интегрирования по частям:

или, что все равно, . При использовании этой формулы приходим к интегралукоторый оказывается проще, чем. Этот метод интегрирования применяется, когда под интегралом стоит произведение разнородных функций, напримери,и,и,ии т. д.

Пример.

.

Здесь обозначили

и вычислили .

Формулу интегрирования по частям иногда приходится применять несколько раз, например:

.

Второе правило  правило замены переменной. Оно задается формулой

, где  дифференцируемая функция от . Функцияподбирается таким образом, чтобы подынтегральное выражение приняло более удобный вид для интегрирования. Выбор ее определяется конкретным видом подынтегрального выражения.

Пример.

Для интегралов вида , где рациональная функция своих аргументов, используется замена:  общий знаменатель дробей .

.

При вычислении этого интеграла сделана замена .

Пример

Рассмотрим интегралы вида , где постоянные, отличные от , а рациональные числа. Первообразная для функции является элементарной функцией в следующих трех случаях:

а)  целое. Тогда имеем случай, рассмотренный в примере 4.

б)  целое. Тогда делаем замену , где знаменатель дроби .

в)  целое. Тогда делаем замену , где знаменатель дроби .

, где .

Здесь сделана замена , поскольку целое.

.

Сделана замена , поскольку целое.

Пример.

Если подынтегральная функция содержит трансцендентную функцию сложного аргумента , то можно сделать замену.

.

Здесь сделана замена . Тогда.

Пример.

Интегралы вида , где рациональная функция своих аргументов, вычисляются с помощью подстановки . При этом имеем.

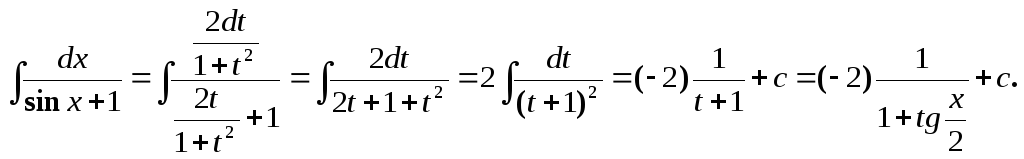Рассмотрим интегрирование функций вида , гдеи многочлены от . Если степень многочленабольше или равна степени многочлена, то делениемнавыделяем целую часть многочлен , т. е., где степень многочленаменьше степени многочлена. Для интегрирования рациональной дроби, называемой правильной, используется разложение этой дроби на сумму простейших дробей. Вид этого разложения зависит от разложенияна множители. Если, где действительные корни многочлена , а трехчленыне имеют действительных корней, то разложение дроби на сумму простейших дробей ищется в виде

,

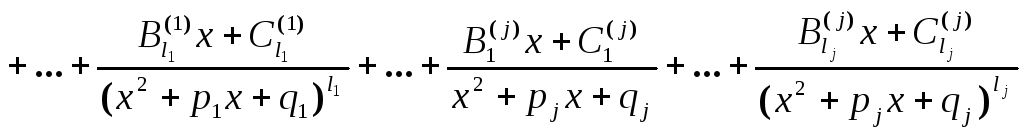где неопределенные коэффициенты находятся следующим образом: правая часть разложения на простейшие дроби приводится к общему знаменателю (им будет многочлен), и у получившегося в числителе многочлена и у многочленаприравниваются коэффициенты при одинаковых степенях. В результате получается система линейных уравнений, из которой находятся неопределенные коэффициенты.

Пример.

Вычислим . Разложение дроби на сумму простейших дробей ищем в виде. Коэффициентыопределяем из равенства

.

Приравнивая коэффициенты при одинаковых степенях , приходим к системе уравнений

Следовательно:

.

Для упрощения вычисления данных интегралов иногда полезно проводить некоторые преобразования, делать замены переменных.

Пример.

.