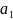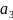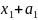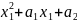- •1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
- •2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
- •3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
- •4.Основная теорема о симметрических многочленах (с док-вом).
- •5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
- •6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
- •7.Возвратные уравнения. Методы их решения.
- •8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
- •9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
- •10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
- •12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
- •13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
- •14.Теорема об изоморфизме фактор-кольцу (с док-вом).
- •15.Теорема об изоморфизме и (с док-вом).
- •16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
- •17.Теорема о представлении (с док-вом).
- •18.Теорема о как линейном n-мерном пространстве (с док-вом).
- •19.Теорема об алгебраическом расширении поля (с док-вом).
- •20.Строение простого трансцендентного расширения поля . Теорема (с док-вом).
- •21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
- •22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
- •23.Теорема о примитивном элементе (с док-вом).
- •24.Поле алгебраических чисел. Теорема 1 (с док-вом).
- •25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
- •26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
- •27.Разрешимость алгебраических уравнений в квадратных радикалах.
- •28.Область рациональности. Теорема (с док-вом).
- •29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
- •30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
- •31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
Рассмотрим
уравнение вида:
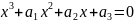 (1) – кубическое уравнение с комплексными
кофиц.
(1) – кубическое уравнение с комплексными
кофиц.
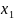 – корень. Уравнение (1) выражается через
квадратные радикалы
– корень. Уравнение (1) выражается через
квадратные радикалы
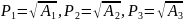 ,
,
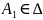 ,
,
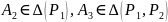 ,
где
,
где
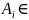 области рациональности.
– корень (1), следовательно
области рациональности.
– корень (1), следовательно
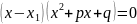 . Используем
схему Горнера.
. Используем
схему Горнера.
|
1 |
|
|
|
|
1 |
|
|
0 |
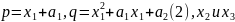 – корни(2),
– корни(2),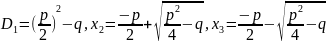 .
выражается
через квадратные радикалы, следовательно
.
выражается
через квадратные радикалы, следовательно
 также выраж., следовательно и
также выраж., следовательно и
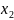 и
и
 .
Если
- корень кубического уравнения, выраж.
через квадратные радикалы, то уравнение
разрешимо в квадратных радикалах, т.е.
и
тоже выражаются в квадратных радикалах.
Т.
Уравнение (1) с комплексными кофиц.
разрешимо в квадратных радикалах тогда
и только тогда, когда один его корень
области рациональности уравнения (1).
(Без
доказательства).
С.
Уравнение (1) с рациональными кофиц.
разрешимо в квадратных радикалах тогда
и только тогда, когда оно имеет хотя бы
один корень рациональный.
.
Если
- корень кубического уравнения, выраж.
через квадратные радикалы, то уравнение
разрешимо в квадратных радикалах, т.е.
и
тоже выражаются в квадратных радикалах.
Т.
Уравнение (1) с комплексными кофиц.
разрешимо в квадратных радикалах тогда
и только тогда, когда один его корень
области рациональности уравнения (1).
(Без
доказательства).
С.
Уравнение (1) с рациональными кофиц.
разрешимо в квадратных радикалах тогда
и только тогда, когда оно имеет хотя бы
один корень рациональный.
30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
Задача. Дан куб и его объем. Найти ребро куба с объемом в 2 раза больше.
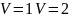
 ребро
ребро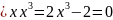
Область
рациональности будет совпадать в полем
.
Пусть это уравнение разрешимо и пусть
- корень. Мы можем построить с помощью
циркуля и линейки корень этого уравнения,
если это уравнение имеет хотя бы один
рациональный корень (из следствия).
Корнем явл.
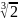 – иррациональное число, следовательно
задача не разрешима.
– иррациональное число, следовательно
задача не разрешима.
31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
Задача. Дан угол . Разделить на три равные части.

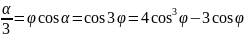
т.к улол
нам дан, то мы можем считать
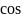 заданным.
заданным.
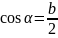
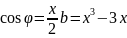
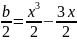
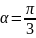 ,
тогда
,
тогда
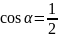
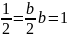
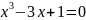 .
Это уравнение не имеет рациональных
корней, слудовательно задача не разрешима.
Данная задача с прямым углом разрешима.
.
Это уравнение не имеет рациональных
корней, слудовательно задача не разрешима.
Данная задача с прямым углом разрешима.