
- •1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
- •2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
- •3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
- •4.Основная теорема о симметрических многочленах (с док-вом).
- •5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
- •6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
- •7.Возвратные уравнения. Методы их решения.
- •8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
- •9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
- •10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
- •12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
- •13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
- •14.Теорема об изоморфизме фактор-кольцу (с док-вом).
- •15.Теорема об изоморфизме и (с док-вом).
- •16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
- •17.Теорема о представлении (с док-вом).
- •18.Теорема о как линейном n-мерном пространстве (с док-вом).
- •19.Теорема об алгебраическом расширении поля (с док-вом).
- •20.Строение простого трансцендентного расширения поля . Теорема (с док-вом).
- •21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
- •22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
- •23.Теорема о примитивном элементе (с док-вом).
- •24.Поле алгебраических чисел. Теорема 1 (с док-вом).
- •25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
- •26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
- •27.Разрешимость алгебраических уравнений в квадратных радикалах.
- •28.Область рациональности. Теорема (с док-вом).
- •29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
- •30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
- •31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
4.Основная теорема о симметрических многочленах (с док-вом).
Т.
Всякий симметр. многочлен
с кофиц. из поля
,
единственным образом представляется
в виде многочл. от основных симметр.
многочл., т.е.
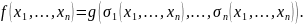 (Доказательства
нет).
(Доказательства
нет).
5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
C.
Пусть дан многочл.
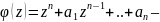 многочлен от одной переменной из
многочлен от одной переменной из
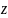 над полем
и дано
над полем
и дано
 это разложение над полем
многочл.
это разложение над полем
многочл.
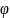 ,
тогда ∀
симметр. многочл.
с кофиц. из поля
,
тогда ∀
симметр. многочл.
с кофиц. из поля
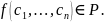 Док.:
В
Док.:
В
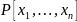 возьмем многочл.
для этого многочл. справедлива Т. (о
симметр. многочл.), т.е.
возьмем многочл.
для этого многочл. справедлива Т. (о
симметр. многочл.), т.е.
 .
По формулам Виета
.
По формулам Виета
 сумма
сумма
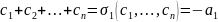 ,
,
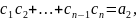 … ,
… ,
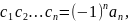 тогда
тогда
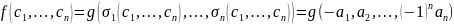 ,
но
,
но
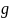 симметр.
многочл. Все
симметр.
многочл. Все
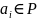 ,
значит
,
значит
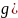 Опр.
многочлен
назыв. однородным, если все его члены
имеют одинаковую степень.
Опр.
многочлен
назыв. однородным, если все его члены
имеют одинаковую степень.
6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
Опр.
Степенной суммой назыв. выражение
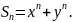 Для
вычисления суммы справедлива след.
формула:
Для
вычисления суммы справедлива след.
формула:
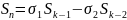 .
Применение
степенных сумм:
.
Применение
степенных сумм:
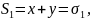
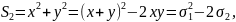
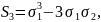
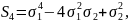
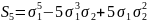 .
Т.
Пусть
.
Т.
Пусть
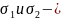 произвольные числа и пусть дано уравнение
произвольные числа и пусть дано уравнение
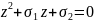 (*), если
(*), если
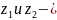 корни этого уравнения, то система
корни этого уравнения, то система
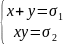 имеет
только 2 решения:
имеет
только 2 решения:
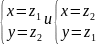 .
Верно и обратное.
.
Верно и обратное.
7.Возвратные уравнения. Методы их решения.
Опр.
Многочл.
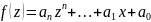 назыв. возвратным, если
назыв. возвратным, если
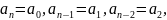 … Опр.
Уравнение
… Опр.
Уравнение
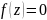 назыв. возвратным, если
назыв. возвратным, если
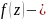 возвратный многочлен. Т.
Всякий возвратный многочл. четной
степени можно представить в виде
возвратный многочлен. Т.
Всякий возвратный многочл. четной
степени можно представить в виде
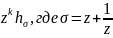 ,
а многочлен нечетной степени делится
на
,
а многочлен нечетной степени делится
на

8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
Рассмотрим
алгебраически замкнутое поле
и в нем 2 многочлена
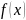 и
и
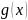 .
Пусть
.
Пусть
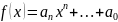 ,
,
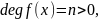 а
а
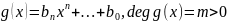 .
.
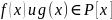 следовательно каждый из этих многочл.
имеют корни. Пусть корнями многочл.
будут
следовательно каждый из этих многочл.
имеют корни. Пусть корнями многочл.
будут
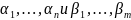 соответственно. Можно доказать, что
соответственно. Можно доказать, что
 имеют общие корни в
тогда и только тогда. когда они не явл.
взаимнопростыми. Опр.
Элемент
имеют общие корни в
тогда и только тогда. когда они не явл.
взаимнопростыми. Опр.
Элемент
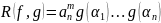 назыв.
результантом многочл.
назыв.
результантом многочл.
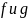 (
(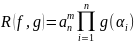 ).
Т.
1)Результант
).
Т.
1)Результант
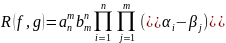 ;
2)
;
2)
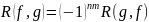 ;
3)
;
3)
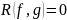 тогда и только тогда, когда
тогда и только тогда, когда
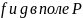 имеют общие корни. Док.:
1)
имеют общие корни. Док.:
1)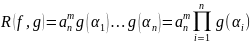 разложим
разложим
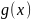 на множители
на множители
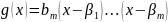 .
.
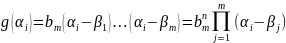 .
.
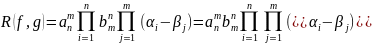 .
2)
.
2)
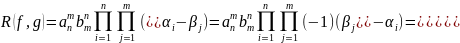
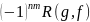 .
3)
.
3)
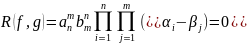 следовательно
следовательно
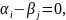
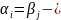 общий
корень
общий
корень

9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
Т.
Результант в форме Сильвестра имеет
вид: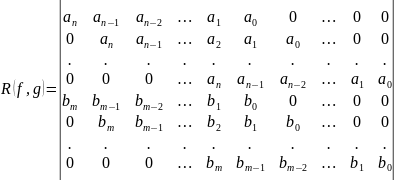 .
Док.:
Для док-ва формулы будем использовать
след. систему уравнений:
.
Док.:
Для док-ва формулы будем использовать
след. систему уравнений:
(*)
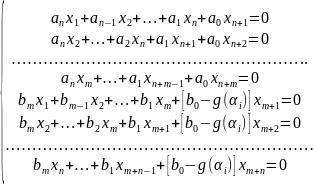
Эта
система явл. системой однородных
уравнений. Покажем что решение системы
(*) будет иметь не 0 значение, а именно:
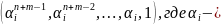 один
из корней многочлена
.
Покажем, что указанный вектор явл.
решением системы (*). Для этого подставим
по корд. в первое уравнение:
один
из корней многочлена
.
Покажем, что указанный вектор явл.
решением системы (*). Для этого подставим
по корд. в первое уравнение:
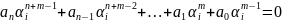 ,
,
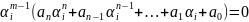 ,
,
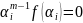 ,
т.к.
,
т.к.
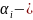 корень
корень
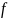 .
Подставим во второе уравнение:
.
Подставим во второе уравнение:
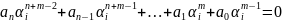 .
Подставим в
.
Подставим в
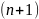 уравнение:
уравнение:
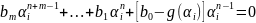 ,
,
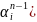 ,
,
 .
Аналогично можно подставить для всех
уравнений, вектор явл. решением. Тем
самым доказано что вектор явл. решением
однородного уравнения с
.
Аналогично можно подставить для всех
уравнений, вектор явл. решением. Тем
самым доказано что вектор явл. решением
однородного уравнения с
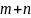 переменными, при чем решение не 0.
переменными, при чем решение не 0.
Система имеет решение тогда и только тогда. когда определитель не равен 0.
10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
Пусть
алгебр. замкнутое поле, в нем дана система
уравнений
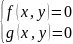 ,
- некоторые многочл. Разложим эти многочл.
по степеням убывания
:
,
- некоторые многочл. Разложим эти многочл.
по степеням убывания
:
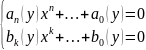 (*).
(*).
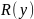 - результант составленный из кофиц.
системы (*
- результант составленный из кофиц.
системы (*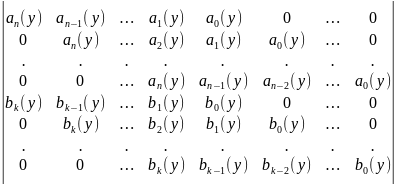 Т.
Если пара
Т.
Если пара
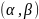 решение системы (*), то
решение системы (*), то
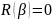 .
Док.:
3 случая. I)
.
Док.:
3 случая. I)
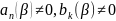 после подстановки в (*):
после подстановки в (*):
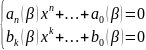 .
Оба многочл. имеют общий корень
.
Оба многочл. имеют общий корень
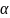 ,
следовательно результант равен 0,
следовательно
.
II)
,
следовательно результант равен 0,
следовательно
.
II)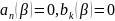 ,
следовательно столбец в результанте
0, следовательно
.
III)
,
следовательно столбец в результанте
0, следовательно
.
III)
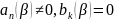 .
(*) примет вид
.
(*) примет вид
 (**) и т.к.
решение системы (**), т.е. явл. корнем
каждого уравнения, то
.
(**) и т.к.
решение системы (**), т.е. явл. корнем
каждого уравнения, то
.
11.Дискриминант. Примеры.
Рассмотрим
алгебр. замкнутое поле
характеристики 0 и кольцо многочл.
 .
Возьмем в
многочл.
,
т.е. у
.
Возьмем в
многочл.
,
т.е. у
 корней
корней
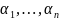 .
.
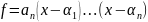 .
Т.
имеет кратные корни тогда и только
тогда, когда
.
Т.
имеет кратные корни тогда и только
тогда, когда
 .
Если
.
Если
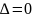 ,
то 0 равно и
,
то 0 равно и
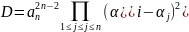 (*).
Опр.
(*) назыв. дискриминантом
.
Если у
есть кратные корни, тогда
(*).
Опр.
(*) назыв. дискриминантом
.
Если у
есть кратные корни, тогда
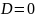 .
Если 2 корния поменять местами в выражении
для
.
Если 2 корния поменять местами в выражении
для
 ,
то
поменяет знак, а
,
то
поменяет знак, а
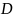 сохранит, т.е.
симметрическая
функция от корней многочл.
.
С.
из основной теоремы о симметр. многочл.
следует, что
можно выразить через кофиц.
:
сохранит, т.е.
симметрическая
функция от корней многочл.
.
С.
из основной теоремы о симметр. многочл.
следует, что
можно выразить через кофиц.
:
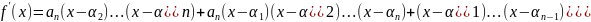 ,
,
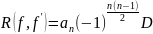 .
.
