
- •1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
- •2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
- •3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
- •4.Основная теорема о симметрических многочленах (с док-вом).
- •5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
- •6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
- •7.Возвратные уравнения. Методы их решения.
- •8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
- •9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
- •10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
- •12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
- •13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
- •14.Теорема об изоморфизме фактор-кольцу (с док-вом).
- •15.Теорема об изоморфизме и (с док-вом).
- •16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
- •17.Теорема о представлении (с док-вом).
- •18.Теорема о как линейном n-мерном пространстве (с док-вом).
- •19.Теорема об алгебраическом расширении поля (с док-вом).
- •20.Строение простого трансцендентного расширения поля . Теорема (с док-вом).
- •21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
- •22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
- •23.Теорема о примитивном элементе (с док-вом).
- •24.Поле алгебраических чисел. Теорема 1 (с док-вом).
- •25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
- •26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
- •27.Разрешимость алгебраических уравнений в квадратных радикалах.
- •28.Область рациональности. Теорема (с док-вом).
- •29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
- •30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
- •31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
Пусть
дано поле
,
рассмотрим элемент
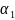 который явл. алгебр. числом
который явл. алгебр. числом
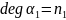 и этот элемент алгебр. число над полем
,
присоединим
к полю
,
мы получим простое алгебр. расширение
и этот элемент алгебр. число над полем
,
присоединим
к полю
,
мы получим простое алгебр. расширение
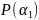 поля
.
Возьмем
поля
.
Возьмем
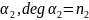 и присоединим к
.
и присоединим к
.
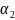 алгебр. число относительно поля
.
Мы получим поле
алгебр. число относительно поля
.
Мы получим поле
 и т.д. В итоге получим
и т.д. В итоге получим
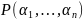 ,
где
,
где
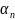 алгебр. число
алгебр. число
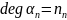 относительно поля
относительно поля
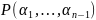 .
З!
Этот элемент
будет алгебр. не только для поля
,
но и для всех предыдущих полей. Опр.
Построенное
расширение поля
назыв. составным расширением поля
,
полученное присоединением к полю
алгебр. чисел степеней соответственно
.
З!
Этот элемент
будет алгебр. не только для поля
,
но и для всех предыдущих полей. Опр.
Построенное
расширение поля
назыв. составным расширением поля
,
полученное присоединением к полю
алгебр. чисел степеней соответственно
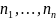 относительно полей
относительно полей
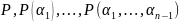 .
Элементы поля
–
.
Элементы поля
–
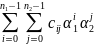 ,
,
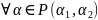 .
по теореме 2 следует, что
.
по теореме 2 следует, что

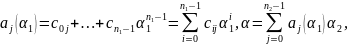
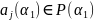 .
Аналогично ∀
элемент
.
Аналогично ∀
элемент
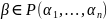 можно представить
можно представить
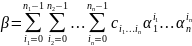 .
Т.
Составное расширение
поля
полученное присоединением к полю
алгебр. чисел
степеней
относительно полей
.
Т.
Составное расширение
поля
полученное присоединением к полю
алгебр. чисел
степеней
относительно полей
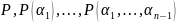 соответственно,
образует линейное пространство над
полем
размерности
соответственно,
образует линейное пространство над
полем
размерности
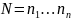 .
Каждый элемент
явл. алгебр. числом степени не выше
.
Каждый элемент
явл. алгебр. числом степени не выше
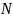 относительно поля
.
(Доказательства нет).
относительно поля
.
(Доказательства нет).
22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
С.1
Все примитивные элементы
явл. алгебр. числами степени не выше чем
относительно поля
.
Док.:
Все эти числа
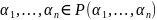 ,
а ∀
элемент из
явл. алгебр. числом степени не выше чем
относительно P.⊠
С.2
Составное расширение
явл. алгебр. расширением поля
.
Док.:
Т.к. ∀
элемент
явл алгебр. числом степени не выше чем
относительно
,
то расширение
явл. алгебр. расширением поля
.⊠
,
а ∀
элемент из
явл. алгебр. числом степени не выше чем
относительно P.⊠
С.2
Составное расширение
явл. алгебр. расширением поля
.
Док.:
Т.к. ∀
элемент
явл алгебр. числом степени не выше чем
относительно
,
то расширение
явл. алгебр. расширением поля
.⊠
23.Теорема о примитивном элементе (с док-вом).
Т.
Составное расширение
поля
явл. простым расширением поля
,
т.е. ∃
алгебр. число
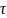 относительно поля
,
такое что
относительно поля
,
такое что
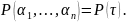 (Доказательства
нет).
(Доказательства
нет).
24.Поле алгебраических чисел. Теорема 1 (с док-вом).
Обозначим
множество всех алгебр. чисел относительно
поля
как
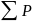 .
Т.
Множество всех алгебр. чисел
отночительно
образуют поле. Док.:
Возьмем ∀
.
Т.
Множество всех алгебр. чисел
отночительно
образуют поле. Док.:
Возьмем ∀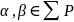 и с помощью этих элементов построим
составное алгебр. расширение.
и с помощью этих элементов построим
составное алгебр. расширение.
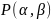 – это расширение, по теореме 2, явл.
простым и все элементы
равны
– это расширение, по теореме 2, явл.
простым и все элементы
равны
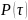 ,
что вытекает из следствия 2. Значит все
элементы из
явл. алгебр. числами относительно
,
но
явл. полем и элементы
,
что вытекает из следствия 2. Значит все
элементы из
явл. алгебр. числами относительно
,
но
явл. полем и элементы
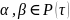 следовательно,
следовательно,
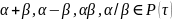 (
(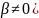 (*), т.е. ∀
,
то и (*) тоже
(*), т.е. ∀
,
то и (*) тоже
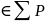 , следовательно на множестве
выполн. операции +, -, *, /, следовательно
числовое поле, следовательно
поле.⊠
, следовательно на множестве
выполн. операции +, -, *, /, следовательно
числовое поле, следовательно
поле.⊠
25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
Т.
Поле
всех алгебр. чисел относительно
явл. алгебр. замкнутым. Док.:
Докажем что корни ∀
многочл. с кофиц. из
,
этому же множеству
.
Рассмотрим многочл.
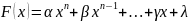 ,
где
,
где
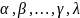 - есть алгебр. числа степеней
- есть алгебр. числа степеней
 соответственно, относительно поля
.
Введем след. обозначения:
соответственно, относительно поля
.
Введем след. обозначения:
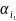 все числа сопряженные с
,
их количество
все числа сопряженные с
,
их количество
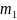 ;
;
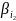 числа сопряженные с
,
их будет
числа сопряженные с
,
их будет
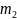 ;
…;
;
…;
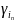 числа сопряженные с
числа сопряженные с
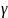 , их будет
, их будет
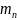 ;
;
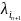 числа сопряженные с λ, их будет
числа сопряженные с λ, их будет
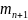 .
Далее составим многочл.:
.
Далее составим многочл.:
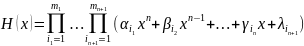 .
Среди множителей, которые входят в
.
Среди множителей, которые входят в
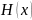 ,
есть и многочлен
,
есть и многочлен
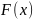 (т.к.
наход. среди сисел сопряженных с
,
т.е. чисел вида
,
среди этих чисел есть
,
и т.д.) Если взять и поменять в
два значения
местами, то от этого многочл.
не изменится, справедливо и для
, и т.д., следовательно кофиц. многочл.
при
этом не изменяются, воспользуемся
следствием из основной теоремы о симметр.
многочл.. Рассмотрим
который явл. многочленом от одной
переменной
,
старший кофиц. равен 1, все кофиц. из поля
.
Тогда всякий симметр. многочл. от корней
будет многочл. от кофиц. многочл.
,
его значения будут
полю
.
Мы получим что кофиц.
не меняются, следовательно они явл.
значениями симметр. многочл. от
(т.к.
наход. среди сисел сопряженных с
,
т.е. чисел вида
,
среди этих чисел есть
,
и т.д.) Если взять и поменять в
два значения
местами, то от этого многочл.
не изменится, справедливо и для
, и т.д., следовательно кофиц. многочл.
при
этом не изменяются, воспользуемся
следствием из основной теоремы о симметр.
многочл.. Рассмотрим
который явл. многочленом от одной
переменной
,
старший кофиц. равен 1, все кофиц. из поля
.
Тогда всякий симметр. многочл. от корней
будет многочл. от кофиц. многочл.
,
его значения будут
полю
.
Мы получим что кофиц.
не меняются, следовательно они явл.
значениями симметр. многочл. от
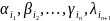 .
По следствию кофиц. многочл.
будут значен. многочл. от кофиц. мнимых
многочл., следовательно они
полю
,
значит корни
есть алгебр. числа относительно
,
и значит они
полю
,
а т.к. многочл.
входит в
в качестве множителя, то и все корни
многочл.
тоже
полю
,
следовательно поле
.
По следствию кофиц. многочл.
будут значен. многочл. от кофиц. мнимых
многочл., следовательно они
полю
,
значит корни
есть алгебр. числа относительно
,
и значит они
полю
,
а т.к. многочл.
входит в
в качестве множителя, то и все корни
многочл.
тоже
полю
,
следовательно поле
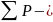 алгебр. замкнуто.⊠
алгебр. замкнуто.⊠
