
- •1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
- •2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
- •3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
- •4.Основная теорема о симметрических многочленах (с док-вом).
- •5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
- •6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
- •7.Возвратные уравнения. Методы их решения.
- •8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
- •9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
- •10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
- •12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
- •13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
- •14.Теорема об изоморфизме фактор-кольцу (с док-вом).
- •15.Теорема об изоморфизме и (с док-вом).
- •16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
- •17.Теорема о представлении (с док-вом).
- •18.Теорема о как линейном n-мерном пространстве (с док-вом).
- •19.Теорема об алгебраическом расширении поля (с док-вом).
- •20.Строение простого трансцендентного расширения поля . Теорема (с док-вом).
- •21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
- •22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
- •23.Теорема о примитивном элементе (с док-вом).
- •24.Поле алгебраических чисел. Теорема 1 (с док-вом).
- •25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
- •26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
- •27.Разрешимость алгебраических уравнений в квадратных радикалах.
- •28.Область рациональности. Теорема (с док-вом).
- •29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
- •30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
- •31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
Опр.
Подмнож.
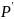 поля
поля
 назыв. Подполем поля
,
если
явл.
полем относит. тех же бинарн. опер. что
и поле
.
Опр.
Поле
назыв. расширением поля
.
Т.1
Кольцо
назыв. Подполем поля
,
если
явл.
полем относит. тех же бинарн. опер. что
и поле
.
Опр.
Поле
назыв. расширением поля
.
Т.1
Кольцо
 многочл. от одной переменной над кольцом
многочл. от одной переменной над кольцом
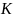 явл. расширением кольца
и содержит переменную
явл. расширением кольца
и содержит переменную
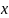 (т.е. кольцо
(т.е. кольцо
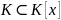 ).
Опр.Число
α назыв. алгебраическим числом (а.ч.)
относительно поля
,
если в кольце многочл.
).
Опр.Число
α назыв. алгебраическим числом (а.ч.)
относительно поля
,
если в кольце многочл.
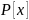 ∃
не 0 многочл.
∃
не 0 многочл.
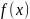 ,
т.ч. α явл. его корнем. Опр.
Число β назыв. трансцендентным (т.ч.)
относительно поля
,
если в кольце многочл.
не ∃
не 0 многочл.
,
т.ч. β явл. его корнем. Опр.
Два многочл.
,
т.ч. α явл. его корнем. Опр.
Число β назыв. трансцендентным (т.ч.)
относительно поля
,
если в кольце многочл.
не ∃
не 0 многочл.
,
т.ч. β явл. его корнем. Опр.
Два многочл.
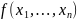 и
и
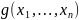 назыв. равными, если у них равны кофиц.
при одинаков. членах. Опр.
Степенью одночл. (монома)
назыв. равными, если у них равны кофиц.
при одинаков. членах. Опр.
Степенью одночл. (монома)
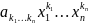 назыв. число
назыв. число
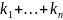 .
Опр.
Степенью многочл. назыв. наивысшая
степень его одночлена. Т.2
Пусть
бесконечная область целостности и
многочлен от
переменных c
кофиц. из
,
если ∀
.
Опр.
Степенью многочл. назыв. наивысшая
степень его одночлена. Т.2
Пусть
бесконечная область целостности и
многочлен от
переменных c
кофиц. из
,
если ∀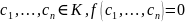 (как функция), то
=0
(как многочлен). (Доказательства
нет).
(как функция), то
=0
(как многочлен). (Доказательства
нет).
2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
Установим
порядок записи для многочл.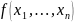 .
Пусть даны два монома:
.
Пусть даны два монома:
 .
Составим разость показателей степени:
.
Составим разость показателей степени:

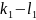
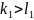 (
(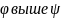 ),
),
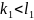 (
(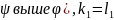 см. след.
см. след.
…
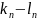
Это
правило отыскания (упоряд.) многочленов
от
переменных. Опр.
Лексикографическим (словарным) упоряд.
многочл. назыв. расположение одночл.
многочл. в порядке убывания высоты
монома. Опр.
Пусть
многочлен
от
переменных
лексикографич. записи, тогда одночл.
стоящий на первом месте в этой записи
назыв. высшим членом многочл.
.
Л.
Если одночл.
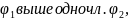 то для ∀
то для ∀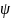 ,
,
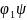 будет выше чем
будет выше чем
 .
Т.
Высший член произвед. двух многочл.
равен произвед. их высших членов.
Док.:рассмотрим
два многочлена
.
Т.
Высший член произвед. двух многочл.
равен произвед. их высших членов.
Док.:рассмотрим
два многочлена
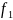 и
и
 .
Пусть
.
Пусть
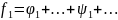 ,
а
,
а
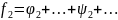 .
.
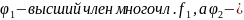 высший член
высший член
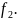 Надо доказать, что высший член многочл.
равен произвед. их высших членов. По
условию
Надо доказать, что высший член многочл.
равен произвед. их высших членов. По
условию
 поэтому для ∀
поэтому для ∀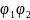 будет выше, чем
будет выше, чем
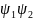 .
.
 ,
поэтому для ∀
,
поэтому для ∀ по лемме
по лемме
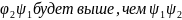 .
Из этого следует, что
.
Из этого следует, что
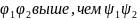 .
.
3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
Опр.
Многочл.
 назыв. симметрическим, если он не
изменится при ∀
перестановке его пересенных. Пример:
назыв. симметрическим, если он не
изменится при ∀
перестановке его пересенных. Пример:
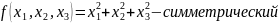 ,
,
 симметрический. Опр.
Высший член симметрического многочл.
назыв. его одночл. наивысшей высоты.
Рассмотрим след. многочл.:
симметрический. Опр.
Высший член симметрического многочл.
назыв. его одночл. наивысшей высоты.
Рассмотрим след. многочл.:
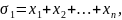
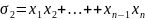 ,
… ,
,
… ,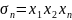 (*). Опр. Многочл. (*) назыв основными
симметрическими многочл. Они порождены
формулами Виета. Т.1
Множ. всех симметр. многочл. над кольцом
образуют подкольцо кольца
(*). Опр. Многочл. (*) назыв основными
симметрическими многочл. Они порождены
формулами Виета. Т.1
Множ. всех симметр. многочл. над кольцом
образуют подкольцо кольца
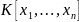 .
Опр.
Полем
назыв. алгебр. замкнутым, если в нем
всякий многочл. имеет корни (в сякий
многочл.
-й
степени имеет точно
корней). Т.2
Пусть
.
Опр.
Полем
назыв. алгебр. замкнутым, если в нем
всякий многочл. имеет корни (в сякий
многочл.
-й
степени имеет точно
корней). Т.2
Пусть
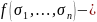 многочл. от элементарных симметр.
многочл., тогда он явл. симметр. многочл.
от переменных
многочл. от элементарных симметр.
многочл., тогда он явл. симметр. многочл.
от переменных
 .
Док.:
Многочл.
.
Док.:
Многочл.
 предст.
собой сумму одночл. явл. произв. основн.
симметр. многочленов. И эти симметр.
многочл. входят в произв. в некотор.
степени. Мы знаем, что
предст.
собой сумму одночл. явл. произв. основн.
симметр. многочленов. И эти симметр.
многочл. входят в произв. в некотор.
степени. Мы знаем, что
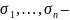 основн. симметр. многочл. от переменных
,
т.к. сумма, произв., разность, степень
симметр. многочл. от
есть симметр. многочл. от
,
то
симметр.
многочл. от переменных
основн. симметр. многочл. от переменных
,
т.к. сумма, произв., разность, степень
симметр. многочл. от
есть симметр. многочл. от
,
то
симметр.
многочл. от переменных

