Канонический вид

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду

,

где a — большая и b — малая полуоси.

Каноническое уравнение параболы

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до д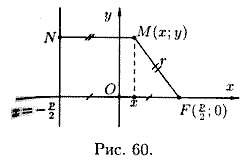 иректрисы называется параметром параболы и обозначается через p (p > 0).

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директри­сой (см. рис. 60). Уравнение директрисы : , фокус — , таким образом начало координат  — середина отрезка . По определению параболы для любой точки , лежащей на ней выполняется равенство . и , тогда равенство приобретает вид: .

После возведения в квадрат и некоторых преобразований получается равносильное уравнение .

Уравнение называется каноническим уравнением параболы. Парабола есть линия второго порядка.