
- •Односторонний предел по Гейне
- •Односторонний предел по Коши
- •Точки разрыва
- •Устранимые точки разрыва
- •Точки разрыва первого и второго рода
- •Свойства Локальные
- •Глобальные
- •Необходимые условия существования локальных экстремумов
- •Достаточные условия существования локальных экстремумов
- •Площадь треугольника
- •Вычисление площади треугольника в пространстве с помощью векторов
- •Простейшие свойства
- •Связанные определения и свойства Подпространство
- •Свойства подпространств
- •Базис. Размерность
- •Линейная оболочка
- •Конечномерный случай
- •Бесконечномерный случай
- •5.1.4. Действия с линейными операторами
- •Канонический вид
Площадь треугольника
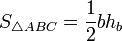 ,
так как
,
так как
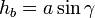 ,
то:
,
то: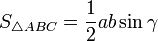
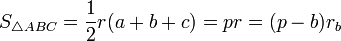
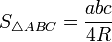
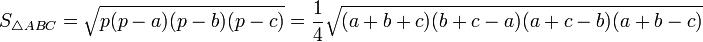 —
формула
Герона
—
формула
Герона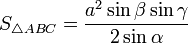
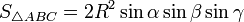
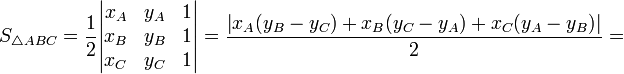
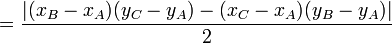
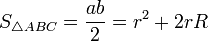 —
для прямоугольного
треугольника
—
для прямоугольного
треугольника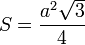 —
для равностороннего
треугольника
—
для равностороннего
треугольника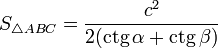 —
если треугольник
задан по стороне и двум прилежащим к
ней углам
—
если треугольник
задан по стороне и двум прилежащим к
ней углам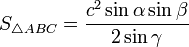 —
если треугольник
задан по стороне и двум прилежащим к
ней углам
—
если треугольник
задан по стороне и двум прилежащим к
ней углам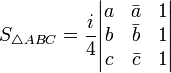 —
ориентированная
площадь треугольника на комплексной
плоскости с вершинами в a, b, c.
—
ориентированная
площадь треугольника на комплексной
плоскости с вершинами в a, b, c.
Где:
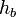 —
высота, проведённая
на сторону
—
высота, проведённая
на сторону
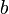 ,
,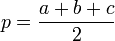 —
полупериметр,
—
полупериметр, —
радиус вписанной
окружности,
—
радиус вписанной
окружности,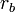 —
радиус вневписанной
окружности,
касающейся стороны
,
—
радиус вневписанной
окружности,
касающейся стороны
,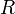 —
радиус описанной
окружности,
—
радиус описанной
окружности,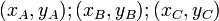 —
координаты вершин
треугольника.
—
координаты вершин
треугольника.
Для площади справедливы неравенства:
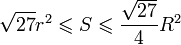 ,
причём оба равенства достигаются.
,
причём оба равенства достигаются.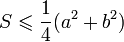 ,
где равенство достигается для
равнобедренного прямоугольного
треугольника.
,
где равенство достигается для
равнобедренного прямоугольного
треугольника.
Вычисление площади треугольника в пространстве с помощью векторов
Пусть
вершины треугольника находятся в точках
![]() ,
,
![]() ,
,
![]() .
.
Введём
вектор площади
![]() .
Длина этого вектора равна площади
треугольника, а направлен он по нормали
к плоскости треугольника:
.
Длина этого вектора равна площади
треугольника, а направлен он по нормали
к плоскости треугольника:
![]()
Положим
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() —
проекции треугольника на координатные
плоскости. При этом
—
проекции треугольника на координатные
плоскости. При этом
![]() и аналогично
и аналогично
![]()
Площадь
треугольника равна
![]() .
.
Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона.
Площадь параллелограмма
![]() ,
где a — сторона, h — высота проведенная
к этой стороне.
,
где a — сторона, h — высота проведенная
к этой стороне.
![]() ,
где a и b — стороны, а
,
где a и b — стороны, а
![]() —
угол между сторонами a и b.
—
угол между сторонами a и b.
![]() .
.
![]() ,
где p — полупериметр, r — радиус вписанной
окружности
,
где p — полупериметр, r — радиус вписанной
окружности
20)
Объём пирамиды может быть вычислен по формуле:
![]()
где
![]() —
площадь
основания и
—
площадь
основания и
![]() —
высота;
—
высота;
Прямой параллелепипед
Объём V=Sо*h
Прямоугольный параллелепипед
Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб
Объём V=a³
21)
Уравнения плоскости
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
Общее уравнение (полное) плоскости
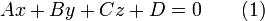
где
![]() и
и
![]() —
постоянные, причём
—
постоянные, причём
![]() и
и
![]() одновременно
не равны нулю; в векторной
форме:
одновременно
не равны нулю; в векторной
форме:![]()
где
![]() —
радиус-вектор точки
—
радиус-вектор точки
![]() ,
вектор
,
вектор
![]() перпендикулярен
к плоскости (нормальный вектор).
Направляющие
косинусы
вектора
перпендикулярен
к плоскости (нормальный вектор).
Направляющие
косинусы
вектора
![]() :
:
![]()
![]()
![]()
Если
один из коэффициентов в уравнении
плоскости равен нулю, уравнение называется
неполным.
При
![]() плоскость
проходит через начало
координат,
при
плоскость
проходит через начало
координат,
при
![]() (или
(или
![]() ,
,
![]() )
П. параллельна оси
)
П. параллельна оси
![]() (соответственно
(соответственно
![]() или
или
![]() ).
При
).
При
![]() (
(![]() ,
или
,
или
![]() )
плоскость параллельна плоскости
)
плоскость параллельна плоскости
![]() (соответственно
(соответственно
![]() или
или
![]() ).
).
Уравнение плоскости в отрезках:
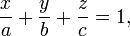
где
![]() ,
,
![]() ,
,
![]() —
отрезки, отсекаемые плоскостью на осях
—
отрезки, отсекаемые плоскостью на осях
![]() и
.
и
.
Уравнение плоскости, проходящей через точку
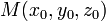 перпендикулярно
вектору нормали
перпендикулярно
вектору нормали
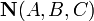 :
:
![]()
в
векторной форме:
![]()
Уравнение плоскости, проходящей через три заданные точки
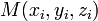 ,
не
лежащие на одной прямой:
,
не
лежащие на одной прямой:
![]()
(смешанное произведение векторов), иначе
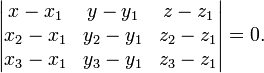
Нормальное (нормированное) уравнение плоскости
![]()
в векторной форме:
![]()
где
![]() -
единичный вектор,
-
единичный вектор,
![]() —
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
—
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
![]()
(знаки
![]() и
противоположны).
и
противоположны).
22)
Векторное параметрическое уравнение прямой в пространстве:
![]()
где
![]() —
радиус-вектор
некоторой фиксированной точки
—
радиус-вектор
некоторой фиксированной точки
![]() лежащей
на прямой,
лежащей
на прямой,
![]() —
ненулевой вектор,
коллинеарный
этой прямой (называемый её направляющим
вектором),
—
ненулевой вектор,
коллинеарный
этой прямой (называемый её направляющим
вектором),
![]() —
радиус-вектор
произвольной точки прямой.
—
радиус-вектор
произвольной точки прямой.
Параметрическое уравнение прямой в пространстве:
![]()
где
![]() —
координаты
некоторой фиксированной точки
лежащей
на прямой;
—
координаты
некоторой фиксированной точки
лежащей
на прямой;
![]() —
координаты
вектора,
коллинеарного
этой прямой.
—
координаты
вектора,
коллинеарного
этой прямой.
Каноническое уравнение прямой в пространстве:
![]()
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой[уточнить] в пространстве:
Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
А1х + В1у + С1 = 0,
А2х + В2у + С2 = 0,
то уравнение прямой можно задать системой этих уравнений:
Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :
![]()
где
фиксированный вектор
![]() ,
ортогональный вектору
,
можно найти, подставляя в это уравнение
радиус-вектор какой-нибудь одной
известной точки прямой.
,
ортогональный вектору
,
можно найти, подставляя в это уравнение
радиус-вектор какой-нибудь одной
известной точки прямой.
23)
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
24)
Пусть
плоскость
![]() задана
уравнением
задана
уравнением
![]() и
дана точка
и
дана точка
![]() .
Тогда расстояние
.
Тогда расстояние
![]() от
точки
от
точки
![]() до
плоскости
определяется
по формуле
до
плоскости
определяется
по формуле
|
(11.7) |
Доказательство.
Расстояние от точки
до
плоскости
-- это, по определению, длина перпендикуляра
![]() ,
опущенного из точки
на
плоскость
(рис. 11.9).
,
опущенного из точки
на
плоскость
(рис. 11.9).

Рис.11.9.Расстояние от точки до плоскости
Вектор
![]() и
нормальный вектор n
плоскости
параллельны,
то есть угол
и
нормальный вектор n
плоскости
параллельны,
то есть угол
![]() между
ними равен 0 или
между
ними равен 0 или
![]() ,
если вектор n
имеет направление противоположное,
указанному на рис. 11.9. Поэтому
,
если вектор n
имеет направление противоположное,
указанному на рис. 11.9. Поэтому
![]()
Откуда
|
(11.8) |
Координаты
точки
![]() ,
которые нам неизвестны, обозначим
,
которые нам неизвестны, обозначим
![]() .
Тогда
.
Тогда
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Раскрыв скобки и перегруппировав
слагаемые, получим
.
Раскрыв скобки и перегруппировав
слагаемые, получим
|
(11.9) |
Точка
лежит
на плоскости
,
поэтому ее координаты удовлетворяют
уравнению плоскости:
![]() .
Отсюда находим, что
.
Отсюда находим, что
![]() .
Подставив полученный результат в
формулу (11.9),
получим
.
Подставив полученный результат в
формулу (11.9),
получим
![]() .
Так как
.
Так как
![]() ,
то из формулы (11.8)
следует формула (11.7).
,
то из формулы (11.8)
следует формула (11.7).
Пусть
плоскости
![]() и
и
![]() заданы
соответственно уравнениями
заданы
соответственно уравнениями
![]() и
и
![]() .
Требуется найти угол
между
этими плоскостями.
.
Требуется найти угол
между
этими плоскостями.
Плоскости,
пересекаясь, образуют четыре двугранных
угла (рис. 11.6): два тупых и два острых или
четыре прямых, причем оба тупых угла
равны между собой, и оба острых тоже
равны между собой. Мы всегда будем искать
острый угол. Для определения его величины
возьмем точку
![]() на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры
на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры
![]() и
и
![]() к
линии пересечения. Нарисуем также
нормальные векторы
к
линии пересечения. Нарисуем также
нормальные векторы
![]() и
и
![]() плоскостей
и
с
началами в точке
(рис.
11.6).
плоскостей
и
с
началами в точке
(рис.
11.6).

Рис.11.6.Угол между плоскостями
Если через точку провести плоскость , перпендикулярную линии пересечения плоскостей и , то прямые и и изображения векторов и будут лежать в этой плоскости. Сделаем чертеж в плоскости (возможны два варианта: рис. 11.7 и 11.8).
 Рис.11.7.Угол
между нормальными векторами острый
Рис.11.7.Угол
между нормальными векторами острый
 Рис.11.8.Угол
между нормальными векторами тупой
Рис.11.8.Угол
между нормальными векторами тупой
В
одном варианте (рис. 11.7)
![]() и
и
![]() ,
следовательно, угол
,
следовательно, угол
![]() между
нормальными векторами равен углу
,
являющемуся линейным углом острого
двугранного угла между плоскостями
и
.
между
нормальными векторами равен углу
,
являющемуся линейным углом острого
двугранного угла между плоскостями
и
.
Во
втором варианте (рис. 11.8)
![]() ,
а угол
между
нормальными векторами равен
,
а угол
между
нормальными векторами равен
![]() .
Так как
.
Так как
![]()
то
в обоих случаях
![]() .
.
По
определению скалярного произведения
![]() .
Откуда
.
Откуда
![]()
и соответственно
|
(11.4) |
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями.
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:
|
(11.5) |
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
|
(11.6) |
Угол между прямыми. Угол между прямой и плоскостью.
Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида
![]() и
и
![]() косинус угла между ними можно найти по
формуле:
косинус угла между ними можно найти по
формуле:
![]() .
(8.14)
.
(8.14)
Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:
![]() -
условие
параллельности прямых,
(8.15)
-
условие
параллельности прямых,
(8.15)
![]() -
условие
перпендикулярности прямых.
(8.16)
-
условие
перпендикулярности прямых.
(8.16)
Угол φ между прямой, заданной каноническими уравнениями
![]() и
плоскостью, определяемой общим уравнением
и
плоскостью, определяемой общим уравнением
Ax + By + Cz + D = 0, можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда
![]() (8.17)
(8.17)
Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:
Al + Bm + Cn = 0, (8.18)
а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m = C/n. (8.19)
25)
Линейное,
или векторное
пространство
![]() над
полем
над
полем
![]() —
это непустое
множество
—
это непустое
множество
![]() ,
на котором введены операции
,
на котором введены операции
сложения, то есть каждой паре элементов множества
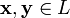 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый
 и
иумножения на скаляр (то есть элемент поля ), то есть любому элементу
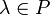 и
любому элементу
и
любому элементу
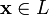 ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый
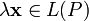 .
.
При этом на операции накладываются следующие условия:
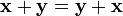 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения);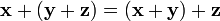 ,
для любых
,
для любых
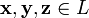 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
 ,
что
,
что
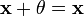 для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;
для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;для любого существует такой элемент
 ,
что
,
что
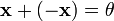 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).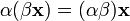 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);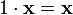 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).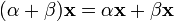 (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров);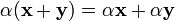 (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества называют векторами, а элементы поля — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
