Необходимые условия существования локальных экстремумов

• Из леммы Ферма вытекает следующее:

Пусть точка является точкой экстремума функции , определенной в некоторой окрестности точки .

Тогда либо производная не существует, либо .

Достаточные условия существования локальных экстремумов

• Пусть функция 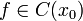непрерывна в 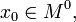и существуют конечные или бесконечные односторонние производные 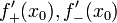. Тогда при условии

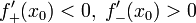
является точкой строгого локального максимума. А если

то является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке

• Пусть функция непрерывна и дважды дифференцируема в точке . Тогда при условии и

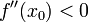
является точкой локального максимума. А если и

то является точкой локального минимума.

13)

Пусть дана квадратная таблица, состоящая из чисел, расположенных в n горизонтальных и в n вертикальных рядах. С помощью этих чисел по определённым правилам вычисляют некоторое число, которое называют определителем n-го порядка и обозначают следующим образом:

                    (1)

Горизонтальные ряды в определителе (1) называют строками, вертикальные – столбцами, числа - элементами определителя (первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит элемент; i = 1, 2, ..., n;  j = 1, 2, ..., n). Порядок определителя – это число его строк и столбцов.

Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы

называется главной диагональю, другая диагональ – побочной.

Определителем n-го порядка называется число, являющееся алгебраической суммой n! членов, каждый из которых – произведение n его элементов, взятых только по одному из каждой n строк и из каждого n столбцов квадратной таблицы чисел, причём половина (определённых) членов берётся с их знаками, а остальные – с противоположными.

Покажем, как вычисляются определители первых трёх порядков.

Определитель первого порядка – это сам элемент т.е.  .

Определитель второго порядка есть число, получаемое следующим образом:                    (2) где

- элементы определителя, а и

- его члены.

Равенство (2) показывает, что со своим знаком берётся член, являющийся произведением элементов главной диагонали, а с противоположным – член, представляющий собой произведение элементов противоположной диагонали.

14)

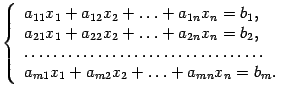(15.1)

(15.2)

(15.3)

(14.13)

 Теорема 14.1   Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица  -- невырожденная, обратная матрица единственна, и справедлива формула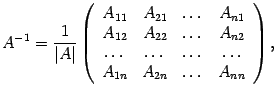 

  Теорема 15.1   (Правило Крамера) Если в системе линейных уравнений с неизвестными , то система имеет решение и притом единственное. Это решение задается формулами

        Доказательство.     По теореме 14.1 обратная матрица находится по формуле

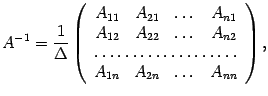
где -- алгебраические дополнения. Тогда из (15.3) следует, что

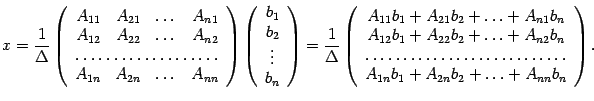
Заметим, что по формуле (14.13) разложение определителя по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому 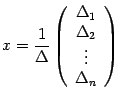, откуда и следует утверждение теоремы.     

15)

 Теорема 14.1   Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица  -- невырожденная, обратная матрица единственна, и справедлива формула 

где  -- алгебраические дополнения к элементам .

        Доказательство.     Так как для невырожденной матрицы правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, что и что . Докажем первое из этих равенств, второе доказывается аналогично.

Пусть . Найдем элементы матрицы , учитывая, что :

Если , то сумма справа равна нулю, то есть при .

Если , то

Сумма справа представляет собой разложение определителя матрицы по -ой строке. Таким образом,

Итак, в матрице диагональные элементы равны 1, а остальные равны нулю, то есть .     

16)

Определение : Скалярное произведение ставит в соответствие паре векторов a и b число (a,b)=|a|·|b|·cosφ_a,b.

Свойства скалярного произведения:

1. коммутативность: (a,b)=(b,a)

2. (а,а)=|а|²

3. (a,b)=0 <=> a b

4. Дистрибутивность: (a₁+а₂,b)= (a₁,b)+ (a₂,b)

5. (а, λ·b)= λ·(a,b) λ R.

Утверждение : В декартовом базисе если а={x₁,y₁,z₁}, b={x₂,y₂,z₂}, то (a,b)=x₁·x₂+y₁·y₂+z₁·z₂.

Определение : Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что

1. | [a,b] |=S_a,b, где S_a,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то S_a,b=0.)

2. a [a,b] b.

3. a, b, [a,b] – правая тройка.

Свойства векторного произведения:

1. [a,b] = -[b,a]

2. [a,b] = θ ó a || b

3. [a₁+a₂,b] = [a₁,b]+[a₂,b]

4. λ·[a,b] = [λ·a,b] = [a,λ·b] λ R.

Утверждение : В декартовой системе координат (базис i, j, k), a={x₁, y₁, z₁}, b={x₂, y₂, z₂}

=> [a,b] = =

 

Определение : Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).

 Утверждение : <a,b,c>=V_a,b,c, если a,b,c – правая тройка, или <a,b,c>= -V_a,b,c, если a,b,c – левая тройка. Здесь V_a,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то V_a,b,c=0.)

 

Утверждение : В декартовой системе координат, если a={x₁, y₁, z₁}, b={x₂, y₂, z₂},

с={x₃, y₃, z₃}, => <a,b,c>= .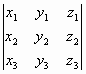

17)

векторы и всегда расположены на одной или параллельных прямых. Такие векторы называются коллинеарными. Справедливо и обратное утверждение: если векторы и коллинеарны, то они связаны соотношением

Два вектора называют ортогональными, если их скалярное произведение равно нулю.

18)

Определение. Векторы   называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно a_i , т.е. .

Если же только при a_i = 0 выполняется , то векторы называются линейно независимыми.

            Свойство 1. Если среди векторов  есть нулевой вектор, то эти векторы линейно зависимы.

            Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

            Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

            Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

            Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

            Свойство 6. Любые 4 вектора линейно зависимы.

19)