
- •Односторонний предел по Гейне
- •Односторонний предел по Коши
- •Точки разрыва
- •Устранимые точки разрыва
- •Точки разрыва первого и второго рода
- •Свойства Локальные
- •Глобальные
- •Необходимые условия существования локальных экстремумов
- •Достаточные условия существования локальных экстремумов
- •Площадь треугольника
- •Вычисление площади треугольника в пространстве с помощью векторов
- •Простейшие свойства
- •Связанные определения и свойства Подпространство
- •Свойства подпространств
- •Базис. Размерность
- •Линейная оболочка
- •Конечномерный случай
- •Бесконечномерный случай
- •5.1.4. Действия с линейными операторами
- •Канонический вид
Свойства Локальные
Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
Если функция непрерывна в точке и
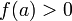 (или
(или
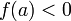 ),
то
),
то
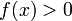 (или
(или
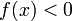 )
для всех
,
достаточно близких к
.
)
для всех
,
достаточно близких к
.Если функции и
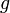 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции
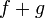 и
и
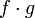 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
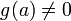 ,
то функция
,
то функция
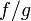 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
 ,
то их композиция
,
то их композиция
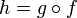 непрерывна
в точке
.
непрерывна
в точке
.
Глобальные
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
Областью значений функции , непрерывной на отрезке
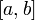 ,
является отрезок
,
является отрезок
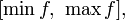 где
минимум и максимум берутся по отрезку
.
где
минимум и максимум берутся по отрезку
.Если функция непрерывна на отрезке и
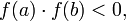 то
существует точка
то
существует точка
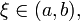 в
которой
в
которой
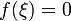 .
.Если функция непрерывна на отрезке и число
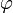 удовлетворяет
неравенству
удовлетворяет
неравенству
 или
неравенству
или
неравенству
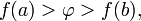 то
существует точка
в
которой
то
существует точка
в
которой
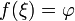 .
.Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
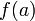 и
и
 .
.Если функции и непрерывны на отрезке , причем
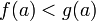 и
и
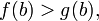 то
существует точка
в
которой
то
существует точка
в
которой
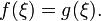 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
9)
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
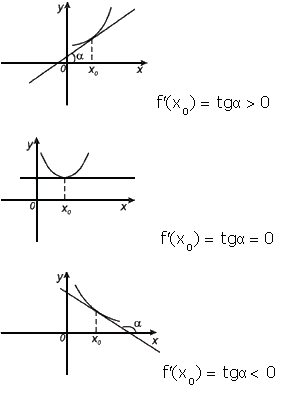
Рассмотрим график функции y = f ( x ):
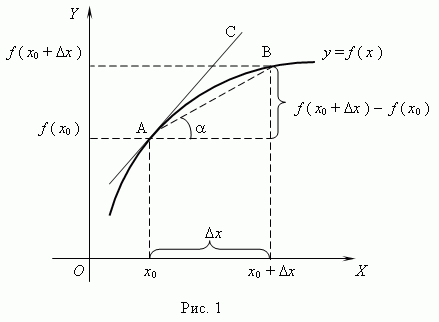
Из
рис.1 видно, что для любых двух точек A
и B
графика функции:
![]() xf(x0+
x)−f(x0)=tg
xf(x0+
x)−f(x0)=tg![]() ,
где
,
где
![]() -
угол наклона секущей AB.
Таким образом, разностное отношение
равно угловому коэффициенту секущей.
Если зафиксировать точку A
и двигать по направлению к ней точку B,
то
-
угол наклона секущей AB.
Таким образом, разностное отношение
равно угловому коэффициенту секущей.
Если зафиксировать точку A
и двигать по направлению к ней точку B,
то
![]() x
неограниченно уменьшается и приближается
к 0, а секущая АВ
приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A.
x
неограниченно уменьшается и приближается
к 0, а секущая АВ
приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A.
10)
Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение y ее представимо в виде
y = f'(x) x + ( x) x,
где первое слагаемое линейно относительно x, а второе является в точке x = 0 бесконечно малой функцией более высокого порядка, чем x. Если f'(x) 0, то первое слагаемое представляет собой главную часть приращения y. Эта главная часть приращения является линейной функцией аргумента x и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.
Определение 5 (дифференциал). Дифференциалом функции y = f(x) называется главная линейная относительно x часть приращения y, равная произведению производной на приращение независимой переменной
dy = f'(x) x.
Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = x. Поэтому формулу для дифференциала принято записывать в следующем виде:
dy = f'(x)dx. |
(4) |
Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол с положительным направлением оси OX, то есть f'(x) = tg . Из прямоугольного треугольника MKN
KN = MNtg xtg = f'(x) x,
то есть dy = KN.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение x.
Отметим основные свойства дифференциала, которые аналогичны свойствам производной.
d c = 0;
d(c u(x)) = c d u(x);
d(u(x) v(x)) = d u(x) d v(x);
d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);
d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v2(x).
Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = (x), то есть рассмотрим сложную функцию y = f((x)). Если каждая из функций f и являются дифференцируемыми, то производная сложной функции согласно теореме (3) равна y' = f'(u)· u'. Тогда дифференциал функции
dy = f'(x)dx = f'(u)u'dx = f'(u)du,
так как u'dx = du. То есть
dy = f'(u)du. |
(5) |
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
Замечание. Отметим, что в формуле (4) dx = x, а в формуле (5) du яляется лишь линейной частью приращения функции u.
11)
Теорема Роля (Ролля).
Если
функция
![]() является
непрерывной на отрезке [a,
b]
и дифференцируемой на интервале (a,
b),
принимает на концах этого интервала
одинаковые значения (т.е.
является
непрерывной на отрезке [a,
b]
и дифференцируемой на интервале (a,
b),
принимает на концах этого интервала
одинаковые значения (т.е.
![]() ),
то на этом интервале найдётся хотя бы
одна точка x=c,
в которой производная функции f(x)
равна нулю, т.е.
),
то на этом интервале найдётся хотя бы
одна точка x=c,
в которой производная функции f(x)
равна нулю, т.е.
![]()
Теорема
Ферма
Пусть
функция
![]() имеет
на множестве
имеет
на множестве
![]() точку
экстремума
точку
экстремума
![]() ,
причём множество
содержит
некоторую
,
причём множество
содержит
некоторую
![]() -окрестность
-окрестность
![]() точки
точки
![]() .
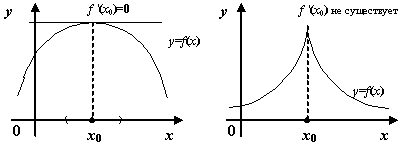
Тогда либо
имеет
в точке
производную,
равную 0, то есть
.
Тогда либо
имеет
в точке
производную,
равную 0, то есть
![]() ,
либо производная в точке
не
существует.
,
либо производная в точке
не
существует.
Теорема
Лагранжа
Пусть
функция
дифференцируема
на интервале
![]() и
непрерывна в точках
и
непрерывна в точках
![]() и
и
![]() .
Тогда найдётся такая точка
.
Тогда найдётся такая точка
![]() ,
что
,
что
|
Теорема
Коши
Пусть
функции
![]() и
и
![]() дифференцируемы
на интервале
дифференцируемы
на интервале
![]() и
непрерывны при
и
непрерывны при
![]() и
и
![]() ,
причём
,
причём
![]() при
всех
при
всех
![]() .
Тогда в интервале
найдётся
такая точка
.
Тогда в интервале
найдётся
такая точка
![]() ,
что
,
что
![]()
12)
лемма Ферма
Пусть
функция
![]() имеет
во внутренней
точке
области
определения
имеет
во внутренней
точке
области
определения
![]() локальный
экстремум.
Пусть также существуют односторонние
производные
локальный
экстремум.
Пусть также существуют односторонние
производные
![]() конечные
или бесконечные. Тогда
конечные
или бесконечные. Тогда
если — точка локального максимума, то
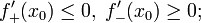
если — точка локального минимума, то
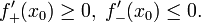
В
частности, если функция
имеет
в
производную,
то
![]()
