
- •Односторонний предел по Гейне
- •Односторонний предел по Коши
- •Точки разрыва
- •Устранимые точки разрыва
- •Точки разрыва первого и второго рода
- •Свойства Локальные
- •Глобальные
- •Необходимые условия существования локальных экстремумов
- •Достаточные условия существования локальных экстремумов
- •Площадь треугольника
- •Вычисление площади треугольника в пространстве с помощью векторов
- •Простейшие свойства
- •Связанные определения и свойства Подпространство
- •Свойства подпространств
- •Базис. Размерность
- •Линейная оболочка
- •Конечномерный случай
- •Бесконечномерный случай
- •5.1.4. Действия с линейными операторами
- •Канонический вид
4)
Рассмотрим
функцию
![]() ,
определённую на некотором множестве
,
определённую на некотором множестве
![]() ,
которое имеет предельную
точку
,
которое имеет предельную
точку
![]() (которая,
в свою очередь, не обязана ему принадлежать).
(которая,
в свою очередь, не обязана ему принадлежать).
Предел функции по Гейне
Значение
![]() называется
пределом
(предельным
значением)
функции
в
точке
,
если для любой последовательности
точек
называется
пределом
(предельным
значением)
функции
в
точке
,
если для любой последовательности
точек
![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений функции
![]() сходится
к
.[1]
сходится
к
.[1]
![]()
Предел функции по Коши
Значение
называется
пределом
(предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа
![]() найдётся
отвечающее ему положительное число
найдётся
отвечающее ему положительное число
![]() такое,
что для всех аргументов
такое,
что для всех аргументов
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .[1]
.[1]
![]()
Окрестностное определение по Коши
Значение
называется
пределом
(предельным
значением)
функции
в
точке
,
если для любой окрестности
![]() точки
существует
выколотая окрестность
точки
существует
выколотая окрестность
![]() точки
такая,
что образ этой окрестности
точки
такая,
что образ этой окрестности
![]() лежит
в
.
Фундаментальное обоснование данного
определения предела можно найти в статье
Предел
вдоль фильтра.
лежит
в
.
Фундаментальное обоснование данного
определения предела можно найти в статье
Предел
вдоль фильтра.
![]()
5)
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
![]()
Расширенное правило суммы
![]()
Предел постоянной величины
Предел
постоянной величины равен самой
постоянной величине:
![]()
Предел произведения функции на постоянную величину
Постоянный
коэффициент можно выносить за знак
предела:
![]()
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
![]()
Расширенное правило произведения
![]()
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
![]()
Предел степенной функции
![]()
где степень p - действительное число. В частности,
![]()
Если
f
( x
) = x,
то
![]()
Предел показательной функции
![]()
где основание a > 0.
Предел логарифмической функции
![]()
где основание a > 0.
Теорема "о двух милиционерах"
Предположим,
что
![]() для
всех x
близких к a,
за исключением, быть может, самой точки
x
= a.
Тогда, если
для
всех x
близких к a,
за исключением, быть может, самой точки
x
= a.
Тогда, если
![]() то
то
![]()
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу L.
6)
Пусть
на некотором числовом
множестве
![]() задана
числовая
функция
задана
числовая
функция
![]() и
число
и
число
![]() —
предельная
точка
области
определения
—
предельная
точка
области
определения
![]() .
Существуют различные определения для
односторонних пределов функции
в
точке
,
но все они эквивалентны.
.
Существуют различные определения для
односторонних пределов функции
в
точке
,
но все они эквивалентны.
Односторонний предел по Гейне
Число
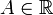 называется
правосторонним
пределом
(правым
пределом,
пределом
справа)
функции
в
точке
,
если для всякой последовательности
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
сходится
к числу
.
называется
правосторонним
пределом
(правым
пределом,
пределом
справа)
функции
в
точке
,
если для всякой последовательности
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
сходится
к числу
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .[1]
![]()
Односторонний предел по Коши
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число
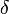 такое,
что для всех точек
из
интервала
такое,
что для всех точек
из
интервала
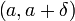 справедливо
неравенство
.
справедливо
неравенство
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число , такое, что для всех точек из интервала
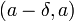 справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
![]()
ε-δ определение непрерывности в точки
Пусть
![]() и
и
![]() .
.
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если для любого
,
если для любого
![]() существует
существует
![]() такое,
что для любого
такое,
что для любого
![]()
Функция
непрерывна
на множестве
![]() ,
если она непрерывна в каждой точке
данного множества.
,
если она непрерывна в каждой точке
данного множества.
В
этом случае говорят, что функция
класса
![]() и
пишут:
и
пишут:
![]() или,
подробнее,
или,
подробнее,
![]()
Точки разрыва
Если
условие, входящее в определение
непрерывности функции в некоторой
точке, нарушается, то говорят, что
рассматриваемая функция терпит
в данной точке разрыв.
Другими словами, если
 —
значение функции
в
точке
,
то предел такой функции (если он
существует) не совпадает с
.
На языке окрестностей условие разрывности
функции
в
точке
получается
отрицанием условия непрерывности
рассматриваемой функции в данной точке,
а именно: существует такая окрестность
точки
области
значений функции
,
что как бы мы близко не подходили к точке
области
определения функции
,
всегда найдутся такие точки, чьи образы
будут за пределами окрестности точки
.
—
значение функции
в
точке
,
то предел такой функции (если он
существует) не совпадает с
.
На языке окрестностей условие разрывности
функции
в
точке
получается
отрицанием условия непрерывности
рассматриваемой функции в данной точке,
а именно: существует такая окрестность
точки
области
значений функции
,
что как бы мы близко не подходили к точке
области
определения функции
,
всегда найдутся такие точки, чьи образы
будут за пределами окрестности точки
.
Устранимые точки разрыва
Если
предел функции существует,
но он не совпадает со значением функции
в данной точке:
![]()
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если
«поправить» функцию
в
точке устранимого разрыва и положить
![]() ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
фукции до непрерывной
или доопределением
фукции по непрерывности,
что и обосновывает название точки, как
точки устранимого
разрыва.
,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
фукции до непрерывной
или доопределением
фукции по непрерывности,
что и обосновывает название точки, как
точки устранимого
разрыва.
7)
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
8)
